
����Ŀ����1����ͼ������4��4�������������У�����2��С�����α�Ϳ��������ֱ�������2��ͼ���ٽ����ɸ��հ�С������Ϳ�ڣ�ʹ��Ϳ�ڵ�ͼ�γ�Ϊ��Գ�ͼ������ͼ��1��Ҫ��ֻ��1���Գ��ᣬͼ��2��Ҫ��ֻ��2���Գ�������

��ֻ��1���Գ��ᣩ ��ֻ��2���Գ��ᣩ
ͼ�� ͼ��
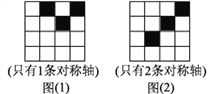
����ͼ��A��BΪֱ��MN�����㣬�ҵ�MN�ľ��벻��ȣ��ֱ���MN����һ��P����������������������ͼ������һ��Pʹ��PA+PB��С�� ����ͼ������һ��Pʹ����PA��PB�������
����д������������ͼ�ۼ���
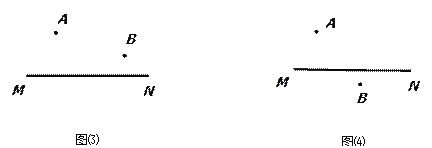
���𰸡�������
�����������������
(1) ����ͼ(1)����ѡ��һ��ֱ����Ϊ����ͼ�εĶԳ������ٽ�����ͼ�ΰ���ѡ��ĶԳ�������Գ���������ͼ��ֻ��һ���Գ��ᣬ��ɰ���ͼ����Ϳ�հ���������ͼ�δ��ڲ�ֻһ���Գ��ᣬ������ѡ��Գ��᳢��. ����ͼ(2)�������ȷ���ԭ��ͼ�εĶԳ��ᣬ����ԭ��ͼ�εĶԳ���Ϊ���գ��۲췽�����ӵ�λ���Ƿ�����ԭͼ�ζԳ��������ı仯���Ӷ�ȷ��ͼ����״.
(2) ����ͼ(3)����һ������Ŀ��������������ԳƵ����ʺ����������߹�ϵ�еġ�����֮�ʹ��ڵ����ߡ��õ���. ������������B����ֱ��MN�ĶԳƵ�B'��Ȼ�������ӵ�B'���A�������߶�AB'��ֱ��MN�Ľ��㼴Ϊ�����P. ����ͼ(4)����һ������Ŀ��������������ԳƵ����ʺ����������߹�ϵ�еġ�����֮��С�ڵ����ߡ��õ���. ������������B����ֱ��MN�ĶԳƵ�B'��Ȼ�����ӵ�B'���A�����ӳ������߶�AB'����ֱ��MN�ཻ���˽��㼴Ϊ�����P.
���������
(1) ��ͼ��ʾ��
(2) ��ͼ��ʾ����P��Ϊ������
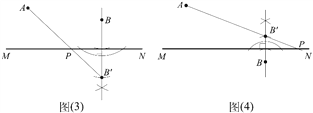
(ע��ͼ�и�����һ�ֳ߹���ͼ�Ľⷨ. ����Ŀ������ȷҪ���ǰ������Ҳ����ʹ�����ǰ�ȹ��߽�����ص���Գ���ͼ.)


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ǡ���ɽ�����۵ķ�Դ�أ���һ��ѧУ��֯���ԡ�ѧϰ��ɽ���ۣ�������̬������Ϊ�����֪ʶ�����У�ij��6��ͬѧ�ijɼ����£���λ���֣���97,99,95,92,92,93������6��ͬѧ�ijɼ�����λ���������ֱ�Ϊ�� ��
A.93�֣�92��B.94�֣�92��
C.94�֣�93��D.95�֣�95��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC,��BAC=64�㣬��BAC��ƽ������AB�Ĵ�ֱƽ���߽��ڵ�O,����C��EF(E��BC�ϣ�F��AC��)�۵�����C���Oǡ���غϣ����OECΪ_________�ȣ�
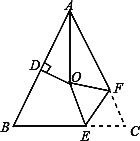
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�ķ���3xn��1+(m��2)x2��5=0��һԪһ�η��̣���m��n��ֵ�ֱ�Ϊ(����)
A. m=1��n=2 B. m=2��n=2 C. m=2��n=1 D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ϻ����ҹ����ϴ��ţ���ͼ��ʾ��ij���ҹ�һ�Һ���ִ�������Ϻ��������ڽ��г�̬��Ѳ������A����ñ�ƫ��30�㷽���ϣ�����Ϊ20�����B����һ�Ҳ������ݵĴ�ֻ���������������У���Ѹ���ر�ƫ��75��ķ���ǰ������Ѳ�飬����һ��ʱ�����C���ɹ����ز�����ֻ�����Һ���ִ������ǰ������Ѳ��Ĺ�������ʻ�˶��ٺ�������������������
���ο����ݣ�cos75��=0.2588��sin75��=0.9659��tan75��=3.732��![]() =1.732��
=1.732��![]() =1.414��
=1.414��
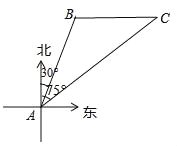
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺������������Ʒ���Ľ������۱��ҵĽ������۸�20Ԫ����֪20������Ʒ�Ľ����ܼ���25������Ʒ�Ľ����ܼ���ͬ��
��1����ס���ÿ����Ʒ�Ľ������ۣ�
��2�����ס���������Ʒ������100����Ҫ��������Ʒ�Ľ����ܼ۲�����9000Ԫ��ͬʱ����Ʒ���������10%��ļ۸����ۣ�����Ʒ���������25%��ļ۸����ۣ�������Ʒȫ�������������ܶ����10480Ԫ�������ļ��ֽ���������
��3����������2���£����Ҳ��ٿ����������أ�������������Ʒȫ�����꣬���ַ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ5����PO=4�����P���O��λ�ù�ϵ�ǣ� ��
A.��P�ڡ�O��
B.��P�ڡ�O��
C.��P�ڡ�O��
D.���ж�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com