
【题目】等腰三角形一腰上的高与另一腰的夹角为 45°,则这个等腰三角形的底角为( )
A.67°B.67.5°C.22.5°D.67.5°或 22.5°
【答案】D
【解析】
先知三角形有两种情况,求出每种情况的顶角的度数,再利用等边对等角的性质(两底角相等)和三角形的内角和定理,即可求出底角的度
解:有两种情况;
(1)如图当△ABC是锐角三角形时,
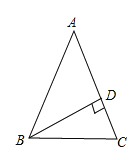
BD⊥AC于D,则∠ADB=90°,已知∠ABD=45°,
∴∠A=90°-45°=45°
∵AB=AC,
∴∠ABC=∠C=![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
(2)如图当△EFG是钝角三角形时,FH⊥EG于H,则∠FHE=90°
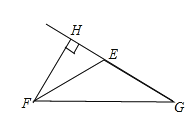
∵∠HFE=45°
∴∠HEF=90°-45°=45°,
∴∠FEG=180°-45°=135°,
∵EF=EG,
∴∠EFG=∠G=![]() (180°-135°)=22.5°.
(180°-135°)=22.5°.
故答案为:D.


科目:初中数学 来源: 题型:
【题目】(1)如图①,正方形![]() 的两边分别在正方形
的两边分别在正方形![]() 的边
的边![]() 和
和![]() 上,连接
上,连接![]() .填空:线段
.填空:线段![]() 与
与![]() 的数量关系为________;直线
的数量关系为________;直线![]() 与
与![]() 所夹锐角的大小为________.
所夹锐角的大小为________.



(2)如图②,将正方形![]() 绕点
绕点![]() 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
(3)把图②中的正方形都换成菱形,且![]() ,如图③,直接写出
,如图③,直接写出![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育,警钟长鸣”,为此某校从14 000名学生中随机抽取了200名学生就安全知识的了解情况进行问卷调查,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计图(如图甲).
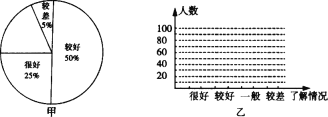
(1)补全扇形统计图,并计算这200名学生中对安全知识了解“较好”、“很好”的总人数;
(2)在图乙中,绘制样本频数的条形统计图;
(3)根据以上信息,请提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:

经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,面积是 (写成多项 式乘法的形式);

(3)比较图1、图2 阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算:(a+b-2c)(a-b+2c).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,三角形ABC的位置如图所示.
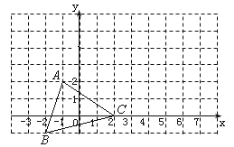
(1)请写出A、B、C三点的坐标;
(2)将三角形ABC向右平移6个单位, 再向上平移2个单位,请在图中作出平移后的三角形A'B'C',并写出三角形A'B'C'各点的坐标;
(3)求出三角形A'B'C'的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)求证:四边形ACPB是平行四边形;
(2)求直线BE的解析式及点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com