
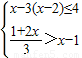
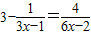 .
. 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:阅读理解
|
|
| 5x+1 |
| 2x-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
.先阅读下面的例题,再按要求解答。(10分)
例:解一元二次不等式x2-9>0
解:∵x2-9=(x+3)(x-3) ∴(x+3)(x-3)>0
由有理数的乘法法则“两数相乘,同号得正”得
(1)![]() (2)
(2)![]()
解不等式组(1),得x>3
解不等式组(2),得x<-3
∴(x+3)(x-3)>0的解集为x>3或x<-3
即一元二次不等式x2-9>0的解集为x>3或x<-3
问题:求分式不等式![]() 的解集
的解集
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建省九年级下学期第一次月考数学卷 题型:解答题
先阅读下面的例题,再按要求解答。(10分)
例:解一元二次不等式x2-9>0
解:∵x2-9=(x+3)(x-3) ∴(x+3)(x-3)>0
由有理数的乘法法则“两数相乘,同号得正”得
(1) (2)
(2)
解不等式组(1),得x>3
解不等式组(2),得x<-3
∴(x+3)(x-3)>0的解集为x>3或x<-3
即一元二次不等式x2-9>0的解集为x>3或x<-3
问题:求分式不等式 的解集
的解集
查看答案和解析>>
科目:初中数学 来源:2012届仙师中学九年级第一次月考试考试数学卷 题型:选择题
.先阅读下面的例题,再按要求解答。(10分)
例:解一元二次不等式x2-9>0
解:∵x2-9=(x+3)(x-3) ∴(x+3)(x-3)>0
由有理数的乘法法则“两数相乘,同号得正”得
(1) (2)
(2)
解不等式组(1),得x>3
解不等式组(2),得x<-3
∴(x+3)(x-3)>0的解集为x>3或x<-3
即一元二次不等式x2-9>0的解集为x>3或x<-3
问题:求分式不等式 的解集
的解集
查看答案和解析>>
科目:初中数学 来源:2012届仙师中学九年级下学期第一次月考考试数学卷 题型:选择题
.先阅读下面的例题,再按要求解答。(10分)
例:解一元二次不等式x2-9>0
解:∵x2-9=(x+3)(x-3) ∴(x+3)(x-3)>0
由有理数的乘法法则“两数相乘,同号得正”得
(1) (2)
(2)
解不等式组(1),得x>3
解不等式组(2),得x<-3
∴(x+3)(x-3)>0的解集为x>3或x<-3
即一元二次不等式x2-9>0的解集为x>3或x<-3
问题:求分式不等式 的解集
的解集
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com