
 如图,∠A+∠B+∠C+∠D+∠E+∠F的和的大小为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F的和的大小为( )| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
分析 连接BE,由三角形内角和外角的关系可知∠C+∠D=∠CBE+∠DEB,由四边形内角和是360°,即可求∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.
解答 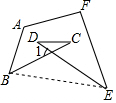 解:如图连接BE.
解:如图连接BE.
∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,
∴∠C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F,
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F,
=∠A+∠ABE+∠BEF+∠F.
又∵∠A+∠ABE+∠BEF+∠F=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.
故选:B.
点评 本题考查的是三角形内角与外角的关系,涉及到四边形及三角形内角和定理,比较简单.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,广场上一个立体雕塑由两部分组成,底座是一个正方体,正上方是一个球体,且正方体的高度和球的高度相等.当阳光与地面的夹角成60°时,整个雕塑在地面上的影子AB长2米,求这个雕塑的高度.(结果精确到百分位,参考数据:$\sqrt{3}$≈1.73)
如图,广场上一个立体雕塑由两部分组成,底座是一个正方体,正上方是一个球体,且正方体的高度和球的高度相等.当阳光与地面的夹角成60°时,整个雕塑在地面上的影子AB长2米,求这个雕塑的高度.(结果精确到百分位,参考数据:$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+2x+1=x(x+2)+1 | B. | 6x4y3=2x2y2•3x2y | ||
| C. | (x+1)(x-1)=x2-1 | D. | x2-4x+4=(x-2)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
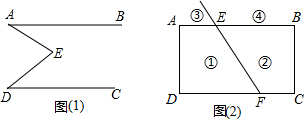
 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 份数/份 | 1 | 2 | 3 | 4 | … |
| 价钱/元 | 0.4 | 0.8 | 1.2 | 1.6 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
| 年消耗费(万元/台) | 1 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com