
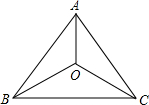
 如图,在△ABC中,AB=AC.BO=CO.求证:AO⊥BC.
如图,在△ABC中,AB=AC.BO=CO.求证:AO⊥BC.  开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 校园小记者就“端午节”知识随机采访了学校50名学生的情况统计图如下:A表示只知道吃粽子,B表示知道吃粽子和纪念屈原,C表示知道吃粽子、纪念屈原和悬挂药材驱瘟病,D表示知道吃粽子、纪念屈原、悬挂药材驱瘟病和赛龙舟.
校园小记者就“端午节”知识随机采访了学校50名学生的情况统计图如下:A表示只知道吃粽子,B表示知道吃粽子和纪念屈原,C表示知道吃粽子、纪念屈原和悬挂药材驱瘟病,D表示知道吃粽子、纪念屈原、悬挂药材驱瘟病和赛龙舟.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com