
 今有总长30米的篱笆,用它围一矩形鸡场,如图,一边靠墙PQ,东侧和南侧各有一门,门宽CD=FG=1米,则当AB为多少米时,矩形鸡场ABEH的面积最大?最大面积是多少?
今有总长30米的篱笆,用它围一矩形鸡场,如图,一边靠墙PQ,东侧和南侧各有一门,门宽CD=FG=1米,则当AB为多少米时,矩形鸡场ABEH的面积最大?最大面积是多少?科目:初中数学 来源: 题型:
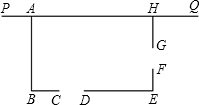 今有总长30米的篱笆,用它围一矩形鸡场,如图,一边靠墙PQ,东侧和南侧各有一门,门宽CD=FG=1米,则当AB为多少米时,矩形鸡场ABEH的面积最大?最大面积是多少?
今有总长30米的篱笆,用它围一矩形鸡场,如图,一边靠墙PQ,东侧和南侧各有一门,门宽CD=FG=1米,则当AB为多少米时,矩形鸡场ABEH的面积最大?最大面积是多少?查看答案和解析>>
科目:初中数学 来源:2011年浙江省金华市兰溪市聚仁学校中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com