
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆![]() 、
、![]() 、
、![]() ,组成一条平滑的曲线,点
,组成一条平滑的曲线,点![]() 从原点
从原点![]() 出发,沿这条曲线向右运动,速度为每秒
出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点
个单位长度,则第2019秒时,点![]() 的坐标是____.
的坐标是____.

【答案】(2019,-1)
【解析】
根据速度及半圆的周长可知点P每秒走![]() 个半圆,分别求出第2、3、4、5、6秒时点P的坐标,可得图象纵坐标4秒一循环,横坐标与移动的时间相同,即可得答案.
个半圆,分别求出第2、3、4、5、6秒时点P的坐标,可得图象纵坐标4秒一循环,横坐标与移动的时间相同,即可得答案.
∵半圆额半径为1,
∴半圆的周长为![]() ×2
×2![]() ×1=
×1=![]() ,
,
∵点P运动速度为每秒![]() 个单位长度,
个单位长度,
∴点P每秒走![]() 个半圆,
个半圆,
∵点P从原点O出发,沿这条曲线向右运动,
∴运动时间为1秒时,点P的坐标为(1,1),
运动时间为2秒时,点P的坐标为(2,0),
运动时间为3秒时,点P的坐标为(3,-1),
运动时间为4秒时,点P的坐标为(4,0),
运动时间为5秒时,点P的坐标为(5,1),
运动时间为6秒时,点P的坐标为(6,0),
…,
∴纵坐标4秒一循环,横坐标与移动的时间相同,
∵2019÷4=504……3,
∴点P2019的坐标为(2019,-1),
故答案为:(2019,-1)


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大;
其中结论正确有 . 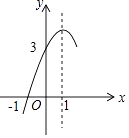
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,点A,B,E分别是x轴和y轴上的任意点. BD是∠ABE的平分线,BD的反向延长线与∠OAB的平分线交于点C.
探究: (1)求∠C的度数.
发现: (2)当点A,点B分别在x轴和y轴的正半轴上移动时,∠C的大小是否发生变化?若不变,请直接写出结论;若发生变化,请求出∠C的变化范围.
应用:(3)如图2在五边形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,CF的反向延长线与∠EDC外角的平分线相交于点P,求∠P的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究学习:
(1)感知与填空
如图,直线![]() .求证:
.求证:![]() .
.
阅读下面的解答过程,并填上适当的理由.
解:延长![]() 交
交![]() 于
于![]() ,
,

∵![]() (已知),∴
(已知),∴![]() ( )
( )
∵![]() ( ),
( ),
∴![]() (等量代换)
(等量代换)
(2)应用与拓展
如图,直线![]() .若
.若![]() ,
,![]() ,
,![]() ,则
,则![]() ______度.
______度.

(3)方法与实践
如图,直线![]() .请探究
.请探究![]() ,
,![]() 和
和![]() 之间有怎样的关系,并证明你的结论.
之间有怎样的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt ABC中,![]() ,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.
,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有足够多的长方形和正方形卡片,如下图:

(1)如果选取1号、2号、3号卡片分别为l张、1张、2张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形(所画图形大小和原图保持一致),并用等式表示拼图前后面积之间的关系:
(2)小明用类似方法解释分解因式a2+5ab+4b2,请画图说明小明的方法(所画图形大小和原图保持一致),并写出分解因式的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 和正方形
和正方形![]() 中,边
中,边![]() 在边
在边![]() 上,
上,![]() 正方形
正方形![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]()
(1)如图2,当![]() 时,求证:
时,求证:![]() ;
;
(2)在旋转的过程中,设![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .①如果存在某一时刻使得
.①如果存在某一时刻使得![]() ,请求出此时
,请求出此时![]() 的长;②若正方形
的长;②若正方形![]() 绕点
绕点![]() 按逆时针方向旋转了
按逆时针方向旋转了![]() ,求旋转过程中,点
,求旋转过程中,点![]() 运动的路径长.
运动的路径长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com