
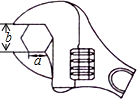
 如图,要拧开一个正六边形螺帽,已知扳手张开的开口b长为2cm,螺帽的边长为a为$\frac{2\sqrt{3}}{3}$cm.
如图,要拧开一个正六边形螺帽,已知扳手张开的开口b长为2cm,螺帽的边长为a为$\frac{2\sqrt{3}}{3}$cm. 分析 根据正六边形的性质,可得∠ABC=120°,AB=BC=a,根据等腰三角形的性质,可得CD的长,根据锐角三角函数的余弦,可得答案.
解答 解:如图:作BD⊥AC于D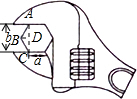 ,
,
由正六边形,得
∠ABC=120°,AB=BC=a,
∠BCD=∠BAC=30°.
由AC=2,得CD=1.
cos∠BCD=$\frac{CD}{BC}$=$\frac{\sqrt{3}}{2}$,即$\frac{1}{a}$=$\frac{\sqrt{3}}{2}$,
解得a=$\frac{2\sqrt{3}}{3}$,
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了正多边形和圆,利用了正六边形的性质得出等腰三角形是解题关键,又利用了正三角形的性质,余弦函数,


科目:初中数学 来源: 题型:选择题
| A. | 2014个 | B. | 2015个 | C. | 4028个 | D. | 6042个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
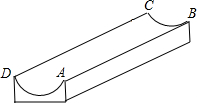 如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)
如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com