
【题目】阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,∠ABC=∠BEF=60°,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC,探究PG与PC的位置关系。
(1)请你写出上面问题中线段PG与PC的位置关系,并说明理由;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明,
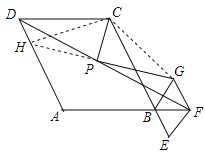
(3)将菱形ABCD和菱形BEFG均改成正方形,如图3,P为DF的中点,此时PG与PC的位置关系和数量关系分别是什么?直接写出答案。



【答案】(1)线段PG与PC的位置关系是PG⊥PC(2)没有发生变化 (3)PG⊥PC,PG=PC
【解析】分析:(1)根据题意可知小颖的思路为,通过判定三角形DHP和PGF为全等三角形来得出证明三角形HCG为等腰三角形且P为底边中点的条件;
(2)思路同上,延长GP交AD于点H,连接CH,CG,本题中除了如(1)中证明△GFP≌△HDP(得到P是HG中点)外还需证明△HDC≌△GBC(得出三角形CHG是等腰三角形).
(3)思路同上,延长GP交CD于H,连接CG,证明△GFP≌△HDP即可.
详解:(1)线段PG与PC的位置关系是PG⊥PC.
理由:延长GP,交CD于点H,
∵四边形ABCD与四边形BEFG是菱形,
∴CD∥AB∥GF,
∴∠PDH=∠PFG,∠DHP=∠PGF,
∵P是线段DF的中点,
∴DP=PF,
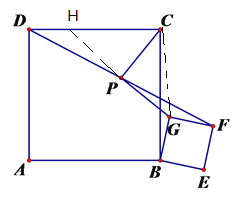
在△DPH和△FGP中,
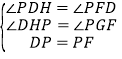 ,
,
∴△DPH≌△FGP(AAS),
∴PH=PG,DH=GF,
∵CD=BC,GF=GB=DH,
∴CH=CG,
∴CP⊥HG,
即PG⊥PC;
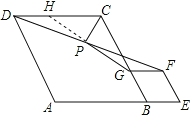
(2)猜想:(1)中的结论没有发生变化.
证明:如图,延长GP交AD于点H,连接CH,CG,
∵P是线段DF的中点,
∴FP=DP,
∵AD∥FG,
∴∠GFP=∠HDP.
又∠GPF=∠HPD,
∴△GFP≌△HDP
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,∠HDC=∠ABC=60°.
由∠ABC=∠BEF=60°,且菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,
∴∠GBC=60°.
∴∠HDC=∠GBC.
∵四边形BEFG是菱形,
∴GF=GB.
∵△HDC≌△GBC.
∴CH=CG.
∴PH=PG,PG⊥PC.
(3)PG⊥PC,PG=PC.


科目:初中数学 来源: 题型:
【题目】如图,Rt⊿ABC中,∠C = 90,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=6,OC=![]() ,则直角边BC的长为___________
,则直角边BC的长为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=![]() ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D. 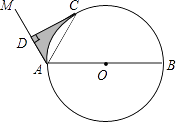
(1)求证:CD是⊙O的切线;
(2)若∠ACD=30°,AD=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1 400辆自行车,平均每天生产200辆.由于各种原因,实际上每天的生产量与计划量相比有出入.表是某周的生产情况(增产为正,减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | ﹣2 | ﹣4 | +13 | ﹣10 | +16 | ﹣9 |
(1)根据记录的数据可知该厂星期五生产自行车 辆;
(2)产量最多的一天比产量最少的一天多生产了 辆自行车;
(3)根据记录的数据可知该厂本周实际生产自行车 辆;
(4)该厂实行计件工资制,每生产一辆得60元,超额完成则每辆奖15元,少生产一辆则扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果保留根号)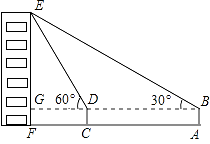
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 ![]() (
( ![]() <
< ![]() <0)与x轴最多有一个交点,现有以下结论:
<0)与x轴最多有一个交点,现有以下结论:
① ![]() <0;②该抛物线的对称轴在y轴左侧;③关于x的方程
<0;②该抛物线的对称轴在y轴左侧;③关于x的方程 ![]() 有实数根;④对于自变量x的任意一个取值,都有
有实数根;④对于自变量x的任意一个取值,都有 ![]() ,其中正确的为( )
,其中正确的为( )
A.①②
B.①②④
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是几次活动汇总后统计的数据:

(1)请估计:当次数s很大时,摸到白球的频率将会接近 ;假如你去摸一次,你摸到白球的概率是 (精确到0.1).
(2)试估算口袋中红球有多少只?
(3)解决了上面的问题后请你从统计与概率方面谈一条启示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com