
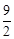 £©£Æ
£©£Æ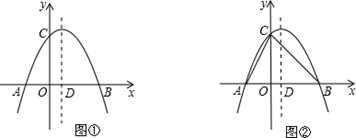
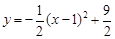 £ª£®2£©¬˙◊„Ãıº˛µƒµ„Pµƒ◊¯±Í”–£∫
£ª£®2£©¬˙◊„Ãıº˛µƒµ„Pµƒ◊¯±Í”–£∫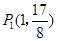 °¢
°¢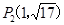 °¢
°¢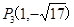 °¢
°¢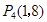 £ª
£ª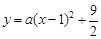 £¨Ω´µ„C£®0£¨4£©¥˙»Îº¥ø…«ÛΩ‚.
£¨Ω´µ„C£®0£¨4£©¥˙»Îº¥ø…«ÛΩ‚.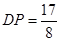 £¨À˘“‘µ„
£¨À˘“‘µ„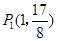 £ª»ÁÕº¢⁄µ±DC=DP ±£∫º¥“‘µ„DŒ™‘≤–ƒ£¨“‘CDµƒ≥§Œ™∞Îæ∂◊˜‘≤£¨ø…“‘∑¢œ÷‘⁄∂‘≥∆÷·…œ”–¡Ω∏ˆ∑˚∫œÃıº˛µƒµ„£¨“ÚŒ™CD=
£ª»ÁÕº¢⁄µ±DC=DP ±£∫º¥“‘µ„DŒ™‘≤–ƒ£¨“‘CDµƒ≥§Œ™∞Îæ∂◊˜‘≤£¨ø…“‘∑¢œ÷‘⁄∂‘≥∆÷·…œ”–¡Ω∏ˆ∑˚∫œÃıº˛µƒµ„£¨“ÚŒ™CD=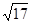 £¨π DP=
£¨π DP=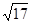 .À˘“‘µ„Pµƒ◊¯±ÍŒ™
.À˘“‘µ„Pµƒ◊¯±ÍŒ™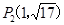 £¨
£¨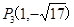 £ª»ÁÕº¢€µ±CD=CP ±£∫µ„C‘⁄DPµƒ¥π÷±∆Ω∑÷œþ…œ£¨π˝µ„C◊˜CE°ÕDPΩª”⁄µ„E£¨¥À ±“◊µ√DE=PE=4£¨À˘“‘µ„Pµƒ◊¯±ÍŒ™
£ª»ÁÕº¢€µ±CD=CP ±£∫µ„C‘⁄DPµƒ¥π÷±∆Ω∑÷œþ…œ£¨π˝µ„C◊˜CE°ÕDPΩª”⁄µ„E£¨¥À ±“◊µ√DE=PE=4£¨À˘“‘µ„Pµƒ◊¯±ÍŒ™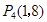 .
.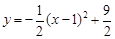 «Ûµ√≈◊ŒÔœþ”Î◊¯±Í÷·µƒΩªµ„◊¯±Í£¨Ω¯∂¯«Ûµ√÷±œþACµƒΩ‚Œˆ ΩŒ™
«Ûµ√≈◊ŒÔœþ”Î◊¯±Í÷·µƒΩªµ„◊¯±Í£¨Ω¯∂¯«Ûµ√÷±œþACµƒΩ‚Œˆ ΩŒ™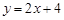 .”…”⁄EF°ŒAC£¨ø…”…∆Ω“∆…Ë≥ˆ÷±œþEFµƒΩ‚Œˆ ΩŒ™
.”…”⁄EF°ŒAC£¨ø…”…∆Ω“∆…Ë≥ˆ÷±œþEFµƒΩ‚Œˆ ΩŒ™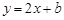 £¨¥À ±ø…«Ûµ√µ„Eµƒ◊¯±ÍŒ™
£¨¥À ±ø…«Ûµ√µ„Eµƒ◊¯±ÍŒ™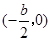 £ÆΩ¯∂¯¡–∑Ω≥Ã◊È«Û≥ˆµ„Fµƒ◊¯±Í£¨◊Ó∫Û¿˚”√
£ÆΩ¯∂¯¡–∑Ω≥Ã◊È«Û≥ˆµ„Fµƒ◊¯±Í£¨◊Ó∫Û¿˚”√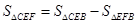 µ√≥ˆ“ª∏ˆπÿ”⁄bµƒ∂˛¥Œ∫Ø ˝£¨¿˚”√∂˛¥Œ∫Ø ˝–‘÷ ø…«Û≥ˆ «∑ҥʑ⁄¬˙◊„Ãıº˛µƒµ„E.
µ√≥ˆ“ª∏ˆπÿ”⁄bµƒ∂˛¥Œ∫Ø ˝£¨¿˚”√∂˛¥Œ∫Ø ˝–‘÷ ø…«Û≥ˆ «∑ҥʑ⁄¬˙◊„Ãıº˛µƒµ„E.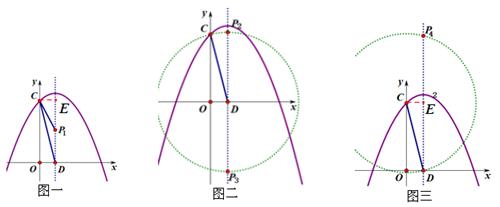
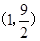
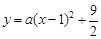
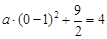 Ω‚µ√
Ω‚µ√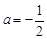
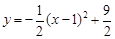 £Æ
£Æ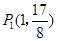 °¢
°¢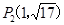 °¢
°¢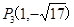 °¢
°¢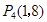
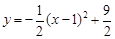
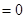
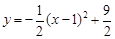 ”Îx÷·µƒΩªµ„Œ™A(-2,0) £¨B (4,0) £Æ
”Îx÷·µƒΩªµ„Œ™A(-2,0) £¨B (4,0) £Æ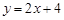 £¨
£¨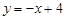 £Æ
£Æ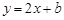 £¨£®-2<x<4£©
£¨£®-2<x<4£©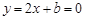 £¨Ω‚µ√
£¨Ω‚µ√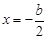 £¨
£¨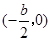 £Æ
£Æ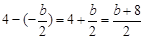 £Æ
£Æ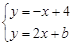 µ√
µ√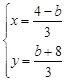 £¨
£¨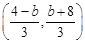 £Æ
£Æ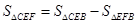
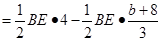
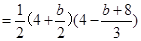
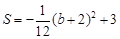
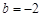 ±£¨S”–◊Ó¥Û÷µ3£¨¥À ±µ„Eµƒ◊¯±ÍŒ™£®1£¨0£©£Æ
±£¨S”–◊Ó¥Û÷µ3£¨¥À ±µ„Eµƒ◊¯±ÍŒ™£®1£¨0£©£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚

| A£Æh=m | B£Æn£æh | C£Æk£æn | D£Æh£æ0£¨k£æ0 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
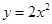 ∑÷±œÚ…œ°¢œÚ”“∆Ω“∆2∏ˆµ•Œª£¨ƒ«√¥–¬≈◊ŒÔœþµƒΩ‚Œˆ Ω «£® £©
∑÷±œÚ…œ°¢œÚ”“∆Ω“∆2∏ˆµ•Œª£¨ƒ«√¥–¬≈◊ŒÔœþµƒΩ‚Œˆ Ω «£® £©A£Æ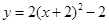 | B£Æ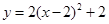 |
C£Æ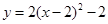 | D£Æ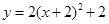 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
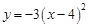 œÚ”“∆Ω“∆3∏ˆµ•Œª≥§∂»µ√µΩµƒ≈◊ŒÔœþ∂‘”¶µƒ∫Ø ˝πÿœµ ΩŒ™
œÚ”“∆Ω“∆3∏ˆµ•Œª≥§∂»µ√µΩµƒ≈◊ŒÔœþ∂‘”¶µƒ∫Ø ˝πÿœµ ΩŒ™A£Æ | B£Æ | C£Æ | D£Æ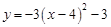 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫ÃÓø’Â
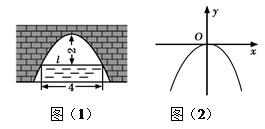
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
 …œ≤ø∑÷µ„µƒ∫·◊¯±Í£¯£¨◊ð◊¯±Íyµƒ∂‘”¶÷µ»Áœ¬±Ì£∫
…œ≤ø∑÷µ„µƒ∫·◊¯±Í£¯£¨◊ð◊¯±Íyµƒ∂‘”¶÷µ»Áœ¬±Ì£∫| £¯ | °≠ |  |  | 0 | 1 | 2 | °≠ |
| y | °≠ | 0 | 4 | 6 | 6 | 4 | °≠ |
 °°°°°°¢⁄≈◊ŒÔœþ”Î
°°°°°°¢⁄≈◊ŒÔœþ”Î ÷·µƒΩªµ„Œ™
÷·µƒΩªµ„Œ™
 °°°°°°°°°°°° ¢Ð‘⁄∂‘≥∆÷·◊Û≤ýyÀÊ£¯‘ˆ¥Û∂¯‘ˆ¥Û
°°°°°°°°°°°° ¢Ð‘⁄∂‘≥∆÷·◊Û≤ýyÀÊ£¯‘ˆ¥Û∂¯‘ˆ¥Û≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
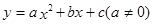 ÕºœÒ»ÁÕºÀ˘ 棨œ¬¡–Ω·¬€£∫¢Ÿ
ÕºœÒ»ÁÕºÀ˘ 棨œ¬¡–Ω·¬€£∫¢Ÿ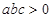 £¨¢⁄
£¨¢⁄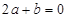 £¨¢€
£¨¢€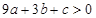 £¨¢Ð∑Ω≥Ã
£¨¢Ð∑Ω≥Ã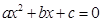 µƒΩ‚ «-2∫Õ4£¨¢ð≤ªµ» Ω
µƒΩ‚ «-2∫Õ4£¨¢ð≤ªµ» Ω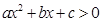 µƒΩ‚ºØ «
µƒΩ‚ºØ «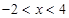 £¨∆‰÷–’˝»∑µƒΩ·¬€”–£® £©
£¨∆‰÷–’˝»∑µƒΩ·¬€”–£® £©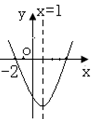
| A£Æ2∏ˆ | B£Æ3∏ˆ | C£Æ4∏ˆ | D£Æ5∏ˆ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
 µƒÕºœÛæ≠π˝µ„
µƒÕºœÛæ≠π˝µ„ ∫Õ
∫Õ £¨œ¬¡–Ω·¬€÷–£∫¢Ÿ
£¨œ¬¡–Ω·¬€÷–£∫¢Ÿ £ª¢⁄
£ª¢⁄ £ª¢€
£ª¢€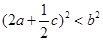 ¢Ð
¢Ð £ª¢ð
£ª¢ð £ª∆‰÷–’˝»∑µƒΩ·¬€”–£® £©∏ˆ
£ª∆‰÷–’˝»∑µƒΩ·¬€”–£® £©∏ˆ
| A£Æ2 | B£Æ3 | C£Æ4 | D£Æ5 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
| A£Æy=£®x©Å1£©2-4 | B£Æy=£®x+1£©2©Å4 |
| C£Æy=£®x-1£©2+2 | D£Æy=£®x+1£©2+2 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com