
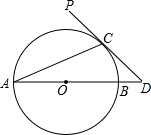
 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.若CD=2,则BD的长为2$\sqrt{2}$-2.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.若CD=2,则BD的长为2$\sqrt{2}$-2. 分析 根据等腰三角形性质和三角形外角性质求出∠COD=2∠A,求出∠D=∠COD,根据切线性质求出∠OCD=90°,求出OC=CD=2,根据勾股定理求出BD即可.
解答 解:∵OA=OC
∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∵∠D=2∠A,
∴∠D=∠COD,
∵PD切⊙O于C,
∴∠OCD=90°,
∴∠D=∠COD=45°
∵CD=2,
∴OC=OB=CD=2,
在Rt△OCD中,由勾股定理得:22+22=(2+BD)2,
解得:BD=2$\sqrt{2}$-2.
故答案为:2$\sqrt{2}$-2.
点评 本题考查了切线的性质,勾股定理,等腰三角形性质,三角形的外角性质的应用,主要考查学生的推理能力.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:选择题
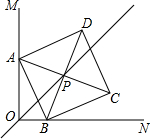 如图,∠MON=90°,线段AB的长是一个定值,点A在射线OM上,点B在射线ON上.以AB为边向右上方作正方形ABCD,对角线AC、BD交于点P,在点A从上往下,点B从左到右运动的过程中,下列说法正确的是( )
如图,∠MON=90°,线段AB的长是一个定值,点A在射线OM上,点B在射线ON上.以AB为边向右上方作正方形ABCD,对角线AC、BD交于点P,在点A从上往下,点B从左到右运动的过程中,下列说法正确的是( )| A. | 点P始终在∠MON的平分线上,且线段OP的长有最大值等于AB | |
| B. | 点P始终在∠MON的平分线上,且线段OP的长有最大值等于$\frac{\sqrt{2}}{2}$AB | |
| C. | 点P不一定在∠MON的平分线上,但线段OP的长有最小值等于AB | |
| D. | 点P不一定在∠MON的角平分线上,但线段OP的长有最小值等于$\frac{\sqrt{2}}{2}$AB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥1 | B. | x≥1且x≠±2 | C. | x≠±2 | D. | x≥1且x≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
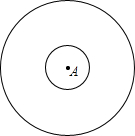 如图,大圆半径为6,小圆半径为2,在如图所示的圆形区域中,随机撒一把豆子,多次重复这个实验,若把“豆子落在小圆区域A中”记作事件W,请估计事件W的概率P(W)的值$\frac{1}{9}$.
如图,大圆半径为6,小圆半径为2,在如图所示的圆形区域中,随机撒一把豆子,多次重复这个实验,若把“豆子落在小圆区域A中”记作事件W,请估计事件W的概率P(W)的值$\frac{1}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
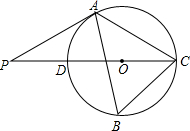 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com