
【题目】如图,在△ABC中,AB=AC,AD是角平分线,BE平分∠ABC交AD于点E,点O在AB上,以OB为半径的⊙O经过点E,交AB于点F 
(1)求证:AD是⊙O的切线;
(2)若AC=4,∠C=30°,求 ![]() 的长.
的长.
【答案】
(1)证明:
如图,连接OE,

∵OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBD,
∴∠OEB=∠EBD,
∴OE∥BD,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠OEA=∠BDA=90°,
∴AD是⊙O的切线
(2)解:∵AB=AC=4,∠C=∠B=30°,
∴BD=2 ![]() ,
,
设圆的半径为r,则BO=OE=r,AO=AC﹣OB=4﹣r,
∵OE∥BD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得r=8
,解得r=8 ![]() ﹣12,
﹣12,
∴ ![]() =
= ![]() =
= ![]()
【解析】(1)连接OE,利用角平分线的定义和圆的性质可得∠OBE=∠OEB=∠EBD,可证明OE∥BD,结合等腰三角形的性质可得AD⊥BD,可证得OE⊥AD,可证得AD为切线;(2)利用(1)的结论,结合条件可求得∠AOE=30°,由(1)可知OE∥BD,设半径为r,则OB=OE=r,AO=4﹣r,在Rt△ABD中,由勾股定理可求得BD,由平行线分线段成比例可得到关于r的方程,可求得圆的半径,利用弧长公式可求得 ![]() .
.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)的相关知识才是答题的关键.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段的中点坐标为![]() .
.
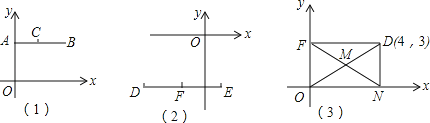
(1)如图(1),C为线段AB中点,A点坐标为(0,4),B点坐标为(5,4),则点C的坐标为
(2)如图(2),F为线段DE中点,D点坐标为(﹣4,﹣3),E点坐标为(1,﹣3).则点F的坐标为________
应用:
(1)如图(3),长方形ONDF的对角线相交于点M,ON,OF分别在x轴和y轴上,O为坐标原点,点D的坐标为(4,3),则点M的坐标为 ;
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与A,B,C构成平行四边形的顶点,直接写出D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是________

查看答案和解析>>
科目:初中数学 来源: 题型:
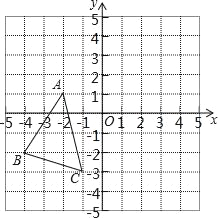
【题目】如图,在平面直角坐标系中,已知A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),把△ABC平移之后得到△A′B′C′,并且C的对应点C′的坐标为(4,1).
(1)分别写出A′、B′两点的坐标;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C. 
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)在(1)的图形中,找出两条相等的线段,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
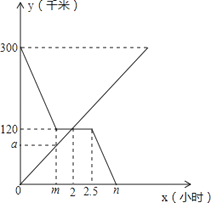
(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1、l2相交于点A(2,3),直线l1与x轴交点B的坐标为(﹣1,0),直线l2与y轴交于点C,已知直线l2的解析式为y=2.5x﹣2,结合图象解答下列问题:
(1)求直线l1的解析式;
(2)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com