
分析 (1)只要证明△OAB是等边三角形即可解决问题.
(2)如图2中,作OK⊥CD于K.只要证明CK=KD,EK=KF即可.
(3)如图3中,作OH⊥CD于K,FK⊥DG于K,GN⊥CD于N,OJ⊥CD于J,OM⊥CG于M.由四边形OFKH是矩形,设OH=x,推出HK=OF=4,OH=FK=x,KD=$\frac{\sqrt{3}}{3}$x,由OH⊥DG,DG=11,推出DH=GH=$\frac{11}{2}$,得到4+$\frac{\sqrt{3}}{3}$x=$\frac{11}{2}$,想办法求出CD、CG、OJ,利用面积法:S△COG+S△COD+S△DOG=S△CDG,求出OM即可解决问题.
解答 解:(1)如图1中,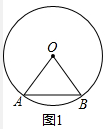
∵OA=OB,AB=OA,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠A=60°,
∴tanA=$\sqrt{3}$.
(2)如图2中,作OK⊥CD于K.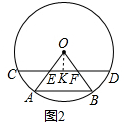
∵OK⊥CD,
∴CK=KD,
∵CD∥AB,
∴∠OEF=∠A=60°=∠AOB,
∴△OEF是等边三角形,
∴OE=OF,∵OK⊥EF,
∴KE=KF,
∴CK-KE=KD-KF,即CE=DF.
(3)如图3中,作OH⊥CD于K,FK⊥DG于K,GN⊥CD于N,OJ⊥CD于J,OM⊥CG于M.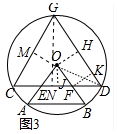
∵△OEF是等边三角形,
∴EF=OF=OE=4,
∵∠OHK=∠FKH=90°,
∵DG∥OB,
∴∠HOF+∠OHK=180°,
∴∠HOF=90°,
∴∠OHK=∠FKH=∠HOF=90°,
∴四边形OFKH是矩形,设OH=x,
∴HK=OF=4,OH=FK=x,KD=$\frac{\sqrt{3}}{3}$x,
∵OH⊥DG,DG=11,
∴DH=GH=$\frac{11}{2}$,
∴4+$\frac{\sqrt{3}}{3}$x=$\frac{11}{2}$,
∴x=$\frac{3}{2}$$\sqrt{3}$,
∴OD=$\sqrt{O{H}^{2}+D{H}^{2}}$=$\sqrt{(\frac{3\sqrt{3}}{2})^{2}+(\frac{11}{2})^{2}}$=$\sqrt{37}$,
∴JD=CJ=$\sqrt{O{D}^{2}-O{J}^{2}}$=$\sqrt{37-12}$=5,CD=2JD=10,
在Rt△GND中,∵DG=11,∠GDN=60°,∠GND=90°,
∴DN=$\frac{11}{2}$,GN=$\frac{11\sqrt{3}}{2}$,CN=CD-DN=$\frac{9}{2}$,
在Rt△CGN中,CG=$\sqrt{C{N}^{2}+G{N}^{2}}$=$\sqrt{(\frac{9}{2})^{2}+(\frac{11\sqrt{3}}{2})^{2}}$=$\sqrt{111}$,
∵S△COG+S△COD+S△DOG=S△CDG,
∴$\frac{1}{2}$$•\sqrt{111}$•OM+$\frac{1}{2}$•10•2$\sqrt{3}$+$\frac{1}{2}$•11•$\frac{3\sqrt{3}}{2}$=$\frac{1}{2}$•10•$\frac{11\sqrt{3}}{2}$,
∴OM=$\frac{\sqrt{37}}{2}$.
点评 本题考查圆综合题、垂径定理、等边三角形的判定和性质、勾股定理、矩形的判定和性质、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,学会利用面积法求距离,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
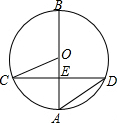 如图,AB是⊙O 的直径,CD是⊙O的一条弦,且CD⊥AB 于点E.
如图,AB是⊙O 的直径,CD是⊙O的一条弦,且CD⊥AB 于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
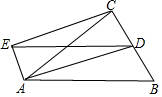 已知:如图,在△ABC中点D为BC边的中点,四边形ABDE为平行四边形.
已知:如图,在△ABC中点D为BC边的中点,四边形ABDE为平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
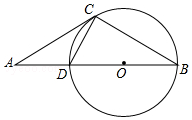 如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD
如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com