
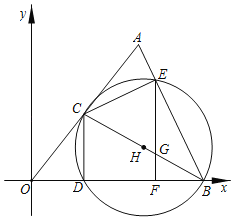
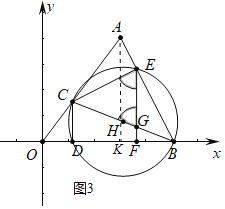
【题目】如图,在平面直角坐标系中,A(3,4),B(5,0),连结AO,AB.点C是线段AO上的动点(不与A,O重合),连结BC,以BC为直径作⊙H,交x轴于点D,交AB于点E,连结CD,CE,过E作EF⊥x轴于F,交BC于G.
(1)AO的长为 ,AB的长为 (直接写出答案)
(2)求证:△ACE∽△BEF;
(3)若圆心H落在EF上,求BC的长;
(4)若△CEG是以CG为腰的等腰三角形,求点C的坐标.
【答案】(1)5,2![]() ;(2)见解析;(3)4;(4)(
;(2)见解析;(3)4;(4)(![]() ,
,![]() ),(
),(![]() ,
,![]() )
)
【解析】
(1)利用两点间距离公式计算即可;
(2)根据两角对应相等的两个三角形相似即可判断;
(3)当GC=GE时,点G与点H重合,根据三角函数和勾股定理解答即可;
(4)分两种情形画出图形,利用锐角三角函数和相似三角形的性质分别求解即可解决问题.
解:(1)∵A(3,4),B(5,0).
∴OA=![]() =5,OB=5,AB=
=5,OB=5,AB=![]() .
.
故答案为:5;2![]() .
.
(2)如图1中,
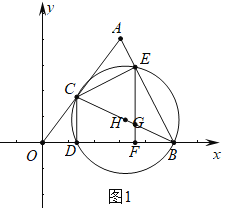
∵OA=OB=5,
∴∠A=∠EBF,
∵BC是直径,
∴∠BEC=∠AEC=90°,
∵EF⊥OB,
∴∠EFB=90°,
∴∠AEC=∠EFB=90°,
∴△ACE∽△BEF;
(3)如图2中,当GC=GE时,点G与点H重合,
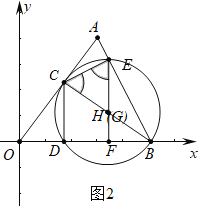
∴GE=GB=GC,
∴∠GEB=∠EBG,
∵∠GEB+∠ABO=90°,
∴∠EBG+∠ABO=90°,
∵OA=OB,
∴∠A=∠OBA,
∴∠A+∠EBG=90°,
∴∠ACB=90°,
∴BC⊥AO,
∴OC=OBcos∠AOB,
∵A(3,4),OA=5,
∴cos∠AOB=![]() ,
,
∴OC=5×![]() =3,
=3,
∴BC=![]() =
=![]() ;
;
(4)①如图2中,当GC=GE时,点G与点H重合,
∴GE=GB=GC,
∴∠GEB=∠EBG,
∵∠GEB+∠ABO=90°,
∴∠EBG+∠
∵OA=OB,
∴∠A=∠OBA,
∴∠A+∠EBG=90°,
∴∠ACB=90°,
∴BC⊥AO,
∵A(3,4),OA=5,
∴cos∠AOB=![]() ,
,
∴OC=OBcos∠AOB=5×![]() =3,
=3,
∴OD= OCcos∠AOB=3×![]() =
=![]() ,CD=
,CD=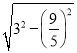 =
=![]() ,
,
∴C(![]() ,
,![]() ).
).
②如图3中,当CE=CG时,作AK⊥OB于K.设CD=4k,OD=3k.
∵A(3,4),B(5,0),
∴AK=4,OK=3,OB=5,BK=2,
∵CE=CG,
∴∠CEG=∠CGE=∠BGF,
∵∠CEG+∠BEF=90°,∠BGF+∠CBD=90°,
∴∠CBD=∠BEF,
∵EF⊥OB,AK⊥OB,
∴EF∥AK,
∴∠BEF=∠BAK,
∴∠CBD=∠BAK,
∵∠CDB=∠AKB=90°,
∴△CBD∽△BAK,
∴![]() ,
,
∴![]() ,
,
∴k=![]() ,
,
∴C(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
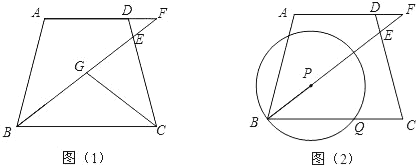
【题目】在等腰梯形ABCD中,AD∥BC,AD=3,AB=CD=4,BC=5,∠B的平分线交DC于点E,交AD的延长线于点F.
(1)如图(1),若∠C的平分线交BE于点G,写出图中所有的相似三角形(不必证明);
(2)在(1)的条件下求BG的长;
(3)若点P为BE上动点,以点P为圆心,BP为半径的⊙P与线段BC交于点Q(如图(2)),请直接写出当BP取什么范围内值时,①点A在⊙P内;②点A在⊙P内而点E在⊙P外.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣mx﹣3x+m﹣4=0(m为常数)
(1)求证:方程有两个不相等的实数根.
(2)设x1,x2是方程的两个实数根,且x1+x2=4,请求出方程的这两个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
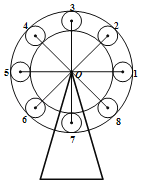
【题目】如图是一个摩天轮,它共有8个座舱,依次标为1~8号,摩天轮中心O的离地高度为50米,摩天轮中心到各座舱中心均相距25米,在运行过程中,当1号舱比3号舱高5米时,1号舱的离地高度为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的各个顶点都在边长为1的正方形网格的交点上.
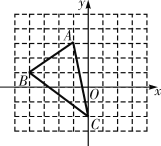
(1)把△ABC绕原点O顺时针旋转90°,作出旋转后的△A1B1C1;
(2)若△A2B2C2与△ABC关于原点O对称,则△A2B2C2的各顶点坐标为:A2 ;B2 ;C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水库大坝的横截面是梯形,坝顶宽5米,CD的长为20![]() 米,斜坡AB的坡度i=1:2.5(i为坡比即BE:AE),斜坡CD的坡度i=1:2(i为坡比即CF:FD),求坝底宽AD的长.
米,斜坡AB的坡度i=1:2.5(i为坡比即BE:AE),斜坡CD的坡度i=1:2(i为坡比即CF:FD),求坝底宽AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com