
【题目】计算:
(1)8+(-![]() )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|-![]() |÷(
|÷(![]() -
-![]() )×(-4)2.
)×(-4)2.
(3)(![]() -
-![]() +
+![]() )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1-![]() )÷3×[2-(-3)2].
)÷3×[2-(-3)2].
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是![]() .
.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB= 90°,CD是∠ACB的平分线,CD的垂直平分线分别交AC,CD,BC于点E ,O,F.求证:四边形CEDF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如果大正方形的面积是13,小正方形的面积是4,直角三角形的较短直角边为a,较长直角边为b,那么![]() 的值为______________.
的值为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点0是AC边上一动点,过点0作DE,使DE∥BC,DE交∠ACB的角平分线于点D,交∠ACB的外角平分线于点E.
(1)求证:OD=OE;
(2)当点0运动到何处时,四边形CDAE是矩形?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?为什么?
(3)探究:腰长为![]() 的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
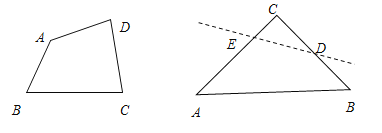
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C是数轴上的三点,点C表示的数是6,点B与点C之间的距离是4,点B与点A的距离是12,点P为数轴上一动点.
(1)数轴上点A表示的数为 .点B表示的数为 ;
(2)数轴上是否存在一点P,使点P到点A、点B的距离和为16,若存在,请求出此时点P所表示的数;若不存在,请说明理由;
(3)点P以每秒1个单位长度的速度从C点向左运动,点Q以每秒2个单位长度从点B出发向左运动,点R从点A以每秒5个单位长度的速度向右运动,它们同时出发,运动的时间为t秒,请求点P与点Q,点R的距离相等时t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com