
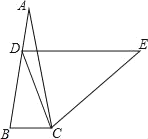
【题目】如图,在等腰△ABC中,AB=AC,∠A=20°.AB上一点D,使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE=_____°.
【答案】70
【解析】
连接AE.根据SAS可证△ADE≌△CBA,可得AE=AC,∠AED=∠BAC=20°,根据等边三角形的判定可得△ACE是等边三角形,根据等腰三角形的判定可得△DCE是等腰三角形,再根据三角形内角和定理和角的和差关系即可求解.
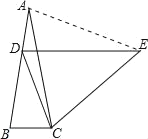
解:如图所示,连接AE.
∵DE∥BC,
∴∠ADE=∠B,
在△ADE与△CBA中, 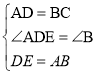
∴△ADE≌△CBA(SAS),
∵AB=AC,∠BAC=20°,
∴AE=AC=AB=DE,∠AED=∠BAC=20°,∠DAE=∠ADE=∠B=∠ACB=80°,
∵∠CAE=∠DAE﹣∠BAC=80°﹣20°=60°,
∴△ACE是等边三角形,
∴CE=AC=AE=DE,∠AEC=∠ACE=60°,
∴△DCE是等腰三角形,
∴∠CDE=∠DCE,
∴∠DEC=∠AEC﹣∠AED=40°,
∴∠DCE=∠CDE=(180﹣40°)÷2=70°.
故答案为:70.


科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字6,-2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树状图的方法,求下列事件的概率:
(1)两次取出小球上的数字相同;
(2)两次取出小球上的数字之和大于10.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前夕,某批发部从厂家购进A、B两种礼盒,已知购进2个A礼盒和3个B礼盒共花520元;购进3个A礼盒和2个B礼盒共花费480元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该批发部经理购进这两种礼盒恰好用去4800元购进A种礼盒最多18个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)已知销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使A、B两种礼盒全部售出后所有方案获利均相同,m的值应是多少?此时这个批发部获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣x+n的图象与反比例函数y=![]() 的图象交于A(4,﹣2),B(﹣2,m)两点.
的图象交于A(4,﹣2),B(﹣2,m)两点.
(1)请直接写出不等式﹣x+n≤![]() 的解集;
的解集;
(2)求反比例函数和一次函数的解析式;
(3)过点A作x轴的垂线,垂足为C,连接BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
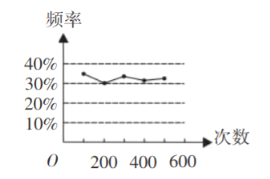
【题目】甲、乙两位同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,给出的 统计图如图所示,则符合这一结果的试验可能是 ( )
A.掷一枚硬币,出现正面朝上的概率
B.掷一枚硬币,出现反面朝上的概率
C.掷一枚骰子,出现 ![]() 点的概率
点的概率
D.从只有颜色不同的两个红球和一个黄球中,随机取出一个球是黄球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,∠AOB=90°,OC平分∠AOB,以C为顶点作∠DCE=90°,交OA于点D,OB于点E.
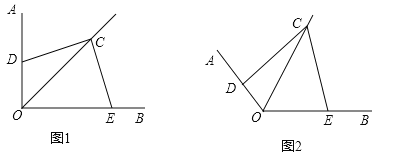
(1)求证:CD=CE;
(2)图1中,若OC=3,求OD+OE的长;
(3)如图2,∠AOB=120°,OC平分∠AOB,以C为顶点作∠DCE=60°,交OA于点D,OB于点E.若OC=3,求四边形OECD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
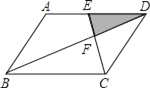
A. 8S B. 9S C. 10S D. 11S
查看答案和解析>>
科目:初中数学 来源: 题型:
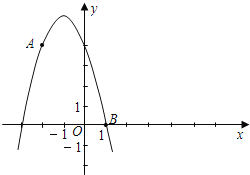
【题目】如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com