
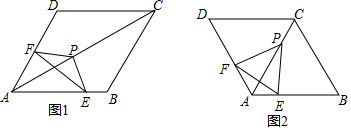
分析 (1)如图1中,作PM⊥AD于M,PN⊥AC于N.由Rt△PMF≌Rt△PNE,推出∠MPF=∠NPE,推出∠EPF=∠MPF,由∠BAD+∠MPN=360°-∠AMP-∠ANP=180°,推出∠EPF+∠BAD=180°即可;
(2)如图2中,作PM⊥AD于M,PN⊥AC于N.由Rt△PMF≌Rt△PNE,推出FM=NE,由PA=PA,PM=PN,推出Rt△PAM≌Rt△PAN,推出AM=AN,推出AF+AE=(AM+FM)+(AN-EN)=2AM,再证明PA=2AM即可解决问题;
(3)结论:AF+AE=PA•cos$\frac{θ}{2}$.证明方法类似(2);
解答 解:(1)如图1中,作PM⊥AD于M,PN⊥AC于N.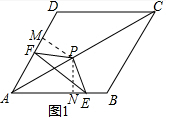
∵四边形ABCD是菱形,
∴∠PAM=∠PAN,
∴PM=PN,
∵PE=PF,
∴Rt△PMF≌Rt△PNE,
∴∠MPF=∠NPE,
∴∠EPF=∠MPF,
∵∠BAD+∠MPN=360°-∠AMP-∠ANP=180°,
∴∠EPF+∠BAD=180°.
(2)如图2中,作PM⊥AD于M,PN⊥AC于N.
由(1)可知Rt△PMF≌Rt△PNE,
∴FM=NE,
∵PA=PA,PM=PN,
∴Rt△PAM≌Rt△PAN,
∴AM=AN,
∴AF+AE=(AM+FM)+(AN-EN)=2AM,
∵∠BAD=120°,
∴∠PAM=60°,易知PA=2AM,
∴AE+AF=PA.
(3)结论:AF+AE=PA•cos$\frac{θ}{2}$.
理由:如图2中,作PM⊥AD于M,PN⊥AC于N.
由(1)可知Rt△PMF≌Rt△PNE,
∴FM=NE,
∵PA=PA,PM=PN,
∴Rt△PAM≌Rt△PAN,
∴AM=AN,
∴AF+AE=(AM+FM)+(AN-EN)=2AM,
∵∠BAD=θ,
∴∠PAM=$\frac{θ}{2}$,易知AM=PA•cos$\frac{θ}{2}$,
∴AF+AE=PA•cos$\frac{θ}{2}$.
点评 本题考查菱形的性质、等边三角形的性质、全等三角形的判定和性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连结AE,交BC于点F,连结AC、BE.
如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连结AE,交BC于点F,连结AC、BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B篮球. C.羽毛球 D.乒乓球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B篮球. C.羽毛球 D.乒乓球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系xOy中,抛物线y=ax2(a≠0)经过点B(-2,4).
如图,平面直角坐标系xOy中,抛物线y=ax2(a≠0)经过点B(-2,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com