
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4) ![]() 中正确的有( )
中正确的有( )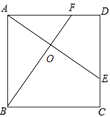
A. 4个
B. 3个
C. 2个
D. 1个
【答案】B
【解析】解:∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠ADE=90°.
∵CE=DF,∴AF=DE.
∴△ABF≌△DAE.
∴AE=BF;
∠AFB=∠AED.
∵∠AED+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AOF=90°,即AE⊥BF;
S△AOB=S△ABF-S△AOF , S四边形DEOF=S△ADE-S△AOF ,
∵△ABF≌△DAE,
∴S△ABF=S△ADE ,
∴S△AOB=S四边形DEOF .
故正确的有 (1)、(2)、(4).
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( ) 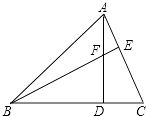
A.40°
B.45°
C.50°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A,B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午2时骑摩托车按同路从A地出发驶往B地,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午行驶的时间t之间的关系.根据图象回答下列问题: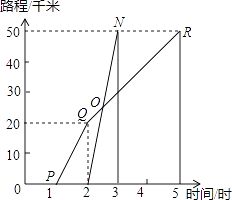
(1)甲在该日下午2﹣5时骑自行车的速度是多少?
(2)乙从出发大约用多长时间就能追上甲?
(3)甲骑自行车和乙骑摩托车在全程的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50° 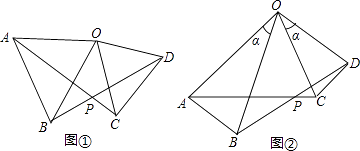
(1)求证:①AC=BD;②∠APB=50°;
(2)如图②,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD间的等量关系为 , ∠APB的大小为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中适合采用普查的是( )
A. 调查市场上某种白酒中塑化剂的含量 B. 调查鞋厂生产的鞋底能承受的弯折次数
C. 了解某城市居民收看新闻联播的情况 D. 了解某火车的一节车厢内感染禽流感病毒的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象. 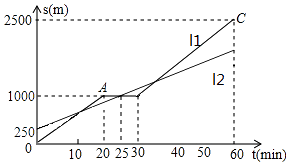
(1)图中线(填l1或l2)表示的是爸爸所走路程与步行时间的函数关系式.
(2)请分别求出l1中BC段以及l2的函数关系式.
(3)请求出小明出发多少时间与爸爸第最后一次相遇.
(4)在速度不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.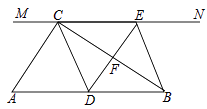
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com