
分析 (1)根据题意用a与b表示这两个两位数,然后列式化简即可求出答案.
(2)①依题意任意一个四位“对称数”的千位数字与个位数字相同,百位数字与十位数字相同,设个位数字为a,百位数字为b,列出式子即可求解.
②依题意任意一个三位“对称数”的百位数字与个位数相同,其个位上的数字为x(1≤x≤4),十位上的数字为y,百位数字为x,列出式子即可求解.
解答 解:(1)设该两位数为:10a+b,
对调后,该两位数为:10b+a,
∴这两个数的和为:10a+b+10b+a=11a+11b=11(a+b)
这两个数的差为:10a+b-(10b+a)=9a-9b=9(a-b)
故这两个数的和能够被11整除,这两个数的差能够被9,
(2)①如:1111,1661;能被11整除,理由如下:
依题意任意一个四位“对称数”的千位数字与个位数字相同,百位数字与十位数字相同,设个位数字为a,百位数字为b,则
四位“对称数”=1000a+100b+10b+a
=1001a+110b=11×(91a+10b)
因为a,b为正整数,所以91a+10b,11×(91a+10b)被11整除.
②依题意任意一个三位“对称数”的百位数字与个位数相同,其个位上的数字为x(1≤x≤4),十位上的数字为y,百位数字为x,则
三位“对称数”=100x+10y+x
=101x+10y=99x+11y+(2x-y)
=11(9x+y)+(2x-y)
因为11(9x+y)+(2x-y)能被11整除,所以2x-y能被11整除,
即2x-y的值为0或11或22,又1≤x≤4,0≤x≤9,所以2x-y=0,
所以y=2x,
所有能被11整除的三位“对称数”为121,242,363,484.
故答案为:(1)11;9
点评 本题考查整式的运算,解题的关键是根据题意列出式子,本题属于中等题型.


科目:初中数学 来源: 题型:选择题
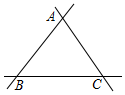 某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )
某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )| A. | 两个角的平分线的交点处 | B. | 两边高线的交点处 | ||
| C. | 两边中线的交点处 | D. | 内部即可 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
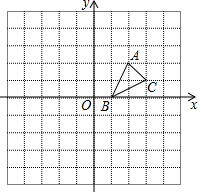 如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1).
如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x-5 | B. | y=x-10 | C. | y=-x-5 | D. | y=-x-10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则A30的坐标是( )
如图,在平面直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则A30的坐标是( )| A. | (4$\sqrt{2}$,-4$\sqrt{2}$) | B. | (-4$\sqrt{2}$,4$\sqrt{2}$) | C. | (-8$\sqrt{2}$,8$\sqrt{2}$) | D. | (30,30) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com