
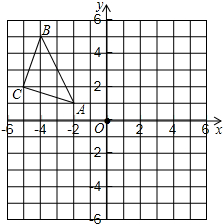
 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).分析 (1)根据轴对称的性质得出对应点的位置,画出图形,写出点A、B、C的对称点A1、B1、C1的坐标即可;
(2)根据图形旋转性质得出对应点的位置,即可画出图形,根据勾股定理求出OA1、OB1的长度,S扇形OB1B2-S扇形OA1A2即为所求.
解答 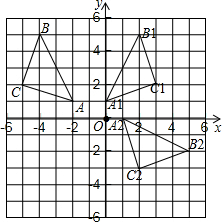 解:(1)如图所示,△A1B1C1即为所求,A1(0,1),B1(2,5),C1(3,2);
解:(1)如图所示,△A1B1C1即为所求,A1(0,1),B1(2,5),C1(3,2);
(2)如图所示,△A2B2C2即为所求,
∵OA1=1,OB1=$\sqrt{29}$,∠A1OA2=∠B1OB2=90°
∴A1B1旋转过程中划过的面积=S扇形OB1B2-S扇形OA1A2=$\frac{90π×(\sqrt{29})^{2}}{360}$-$\frac{90π×{1}^{2}}{360}$=7π.
点评 本题考查了轴对称和图形的旋转以及扇形面积的求法,求出对应点的位置是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:填空题
关于x的方程 的解是正数,则a的取值范围是_________.
的解是正数,则a的取值范围是_________.
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
(12分)某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
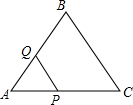 如图,在等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以1cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )
如图,在等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以1cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )| A. | 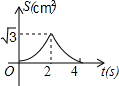 | B. | 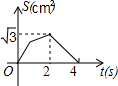 | C. | 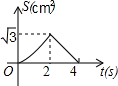 | D. | 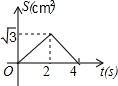 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=4,AD=2,点P、Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P、Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x(秒),△APQ的面积为S(平方单位),则△APQ的面积S与运动时间x之间的函数图象大大致形状是( )
如图,在矩形ABCD中,AB=4,AD=2,点P、Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P、Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x(秒),△APQ的面积为S(平方单位),则△APQ的面积S与运动时间x之间的函数图象大大致形状是( )| A. | 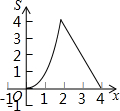 | B. | 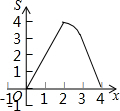 | C. | 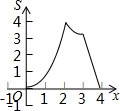 | D. | 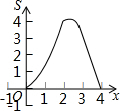 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com