
分析 (1)利用异分母分式的加减的逆用即可;
(2)①根据(1)的规律即可得出结论;
②根据(1)的规律即可得出结论.
解答 解:(1)$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$,
故答案为$\frac{1}{n}-\frac{1}{n+1}$,
(2)①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…-$\frac{1}{2015}$
=1-$\frac{1}{2015}$
=$\frac{2014}{2015}$,
故答案为$\frac{2014}{2015}$;
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…-$\frac{1}{n+1}$
=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$,
故答案为$\frac{n}{n+1}$.
点评 此题是规律型--数字的变化类,主要考查了异分母分式的加减的逆用,寻找规律是解本题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:填空题
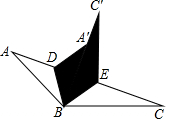 如图所示,将一张三角形纸片分别沿着BD,BE对折,使点C落在点C′,点A落在点A′,点B,A′,C′在同一条直线上,若∠ABC=130°,则∠DBE=65度.
如图所示,将一张三角形纸片分别沿着BD,BE对折,使点C落在点C′,点A落在点A′,点B,A′,C′在同一条直线上,若∠ABC=130°,则∠DBE=65度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
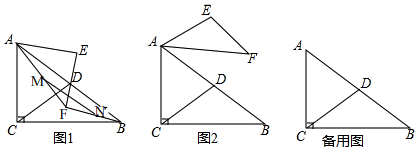
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
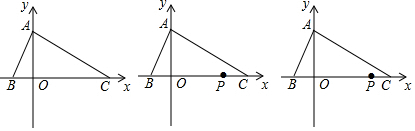
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com