

分析 (1)由横纵为时间,纵轴为距离,可得出下图反映了距离与时间之间的关系;
(2)由20分钟到30分钟内,距离没有发生变化,可猜测爷爷从家里出发后20分钟到30分钟可能在原地锻炼;
(3)横坐标最大值为45,由此即可得出爷爷每天散步45分钟;
(4)纵坐标最大值为900,由此即可得出爷爷散步时最远离家900米;
(5)由速度=路程÷时间,即可求出爷爷离开家后的20分钟内的平均速度.
解答 解:(1)下图反映了距离与时间之间的关系.
(2)∵20分钟到30分钟内,距离没有发生变化,
∴爷爷从家里出发后20分钟到30分钟可能在原地锻炼.
(3)∵当45分钟时,爷爷回到家,
∴爷爷每天散步45分钟.
(4)∵纵坐标的最大值为900,
∴爷爷散步时最远离家900米.
(5)900÷20=45(米/分钟),
∴爷爷离开家后的20分钟内的平均速度为45米/分钟.
点评 本题考查了函数图象,解题的关键是:(1)找出横纵代表时间,纵轴代表距离;(2)根据函数图象找出该时间段距离没有变化;(3)找出横坐标的最大值;(4)找出纵坐标的最大值;(5)根据速度=路程÷时间列式计算.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:填空题
 如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是直角三角形,直角顶点A1,A2,…,An在x轴上,且OA1=A1A2,OA2=A2A3,…,OAn=AnAn+1,点B1,B2,…,Bn在直线y=2x上,已知点A1坐标为(1,0),则点B2017的坐标为(22016,22017).
如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是直角三角形,直角顶点A1,A2,…,An在x轴上,且OA1=A1A2,OA2=A2A3,…,OAn=AnAn+1,点B1,B2,…,Bn在直线y=2x上,已知点A1坐标为(1,0),则点B2017的坐标为(22016,22017).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
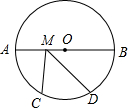 如图,⊙O的半径是8,AB是⊙O的直径,M为AB上一动点,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,则CM+DM的最小值为16.
如图,⊙O的半径是8,AB是⊙O的直径,M为AB上一动点,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,则CM+DM的最小值为16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com