
分析 (1)根据当n为奇数时,第n个数为$\frac{1}{n+1}$;当n为偶数时,第n个数为-$\frac{n}{n+1}$,解答即可;
(2)根据数字变化规律得出变化趋势.
解答 解:(1)由数列可知,当n为奇数时,第n个数为$\frac{1}{n+1}$;当n为偶数时,第n个数为-$\frac{n}{n+1}$;
∴第9个数为$\frac{1}{10}$,第14个数为-$\frac{14}{15}$,第99个数为$\frac{1}{100}$,第2012个数为-$\frac{2012}{2013}$,
故答案为:$\frac{1}{10}$,-$\frac{14}{15}$,$\frac{1}{100}$,-$\frac{2012}{2013}$;
(2)由(1)知,当n为奇数时,n无限大时,$\frac{1}{n+1}$接近于0;若n为偶数,n无限大时,-$\frac{n}{n+1}$接近于-1,
故如果这一组数据无限排列下去,与0和-1越来越接近.
点评 此题主要考查了数字变化类,根据已知注意数字中的变与不变是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
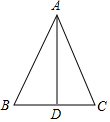 如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为( )
如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
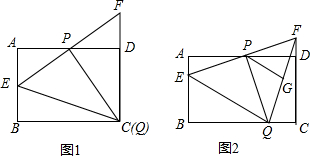
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com