
 轴对称的点的坐标是 .
轴对称的点的坐标是 . 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源:不详 题型:单选题
| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| v | -6.10 | -2.90 | -2.01 | -1.51 | -1.19 | -1.05 | -0.86 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 月销量x(件) | 1500 | 2000 |
| 销售价格y(元/件) | 185 | 180 |
 (元)
(元) x2元的附加费,设月利
x2元的附加费,设月利 (元)(利润=销售额-成本-附加费).
(元)(利润=销售额-成本-附加费). ,
, 与x间的函数关系式(不必写x的取值范围);
与x间的函数关系式(不必写x的取值范围);查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
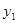 (万元)之间满足关系式
(万元)之间满足关系式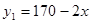 ,月产量x(套)与生产总成本
,月产量x(套)与生产总成本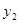 (万元)存在如图所示的一次函数关系.
(万元)存在如图所示的一次函数关系.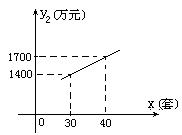
 与x之间的函数关系式;
与x之间的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 =
= 代入,这个函数将失去意义,我们把这样的数值
代入,这个函数将失去意义,我们把这样的数值 叫做自变量x的奇异值,请写出一个函数,使2和-2都是这个函数的奇异值,你写出的函数为 ▲ .
叫做自变量x的奇异值,请写出一个函数,使2和-2都是这个函数的奇异值,你写出的函数为 ▲ .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 立方米,水费为
立方米,水费为 元,则
元,则 与
与 的函数关系用图象表示正确的是( )
的函数关系用图象表示正确的是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com