
【题目】已知:如图所示,在△ABC中,∠BAC=60°,AD=AE,BE、CD交于点F,且∠DFE=120°.在BE的延长线上截取ET=DC,连接AT.
(1)求证:∠ADC=∠AET;
(2)求证:AT=AC;
(3)设BC边上的中线AP与BE交于Q.求证:∠QAB=∠QBA.

【答案】(1)见解析 (2)见解析 (3)见解析
【解析】
(1)根据已知条件求得∠AEF+∠ADC=180°,再根据∠AEF+∠AET=180°即可得∠ADC=∠AET;
(2)利用SAS可证△AET≌△ADC即可解答;
(3)延长AP至G点,使得GP=AP,连接BG.,再利用SAS可证△APC≌△GPB的性质证明出△ABG≌△BAT即可解答.
(1)∵∠BAC=60°,∠DFE=120°,
∴∠AEF+∠ADC=360°-60°-120°=180°.
∵∠AEF+∠AET=180°
∴∠ADC=∠AET.
(2)利用SAS可证△AET≌△ADC.
∴AT=AC.
(3)延长AP至G点,使得GP=AP,连接BG.
利用SAS可证△APC≌△GPB.
∴AC=GB
由(2)可知AC=AT
∴GB=AT
由(2)可知∠TAC=∠CAD=60°
∴∠TAB=120°
又∵△APC≌△GPB,∴∠CAP=∠BGP,∴AC∥BG
∴∠ABG=180°-∠BAC=180°-60°=120°=∠TAB
利用SAS可证△ABG≌△BAT,
∴∠QAB=∠QBA.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.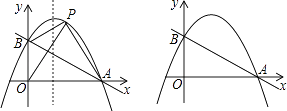
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的 ![]() 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠A=70°,∠B=90°,点A关于BC的对称点是A',点B关于AC的对称点是B',点C关于AB的对称点是C',若△ABC的面积是![]() ,则△A'B'C'的面积是_________________________.
,则△A'B'C'的面积是_________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1: ![]() .
.
(1)求新坡面的坡角a;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是放在地面上的一个长方体盒子,其中AB=9cm,BC=6cm,BF=5cm,点M在棱AB上,且AM=3cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )

A. 10cm B. ![]() C.
C. ![]() D. 9cm
D. 9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 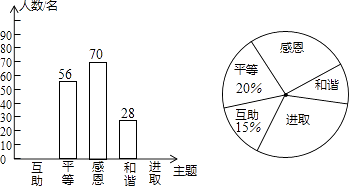
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两外角平分线交于点P,易证∠P=90°-![]() ∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+
∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+![]() ∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
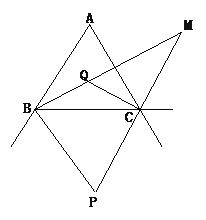
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com