
【题目】如图所示,在菱形ABCD中,∠BAD=120°,AB=4.求: 
(1)对角线AC,BD的长;
(2)菱形ABCD的面积.
【答案】
(1)解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAD=120°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∵四边形ABCD是菱形,
∴AC⊥BD,A0=2,
∴OD= ![]() =
= ![]() =2
=2 ![]() ,
,
∴BD=4 ![]()
(2)解:面积为 ![]() AC×BD=
AC×BD= ![]() =8
=8 ![]()
【解析】(1)根据菱形的性质可得AB=BC,然后再证明△ABC是等边三角形,从而可得AC=AB=4,进而可得AO=2,再利用勾股定理计算BO长,进而可得BD长;(2)利用菱形的面积= ![]() ab(a、b是两条对角线的长度)可得面积.
ab(a、b是两条对角线的长度)可得面积.
【考点精析】利用菱形的性质对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


科目:初中数学 来源: 题型:
【题目】若一粒米的质量约是0.0000021 kg,将数据0.0000021用科学记数法表示为( )
A. 21×10-5B. 2.1×10-7C. 2.1×10-5D. 2.1×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC=m,AB=3m,AC=n.
(1)将△ABC绕点B逆时针旋转,使点C落在AB边上的点C1处,点A落在点A1处,在图中画出△A1BC1;
(2)求四边形ACBA1的面积;(用m、n的代数式表示)
(3)将△A1BC1沿着AB翻折得△A2BC1,A2C1交AC于点D,写出四边形BCDC1与三角形ABC的面积的比值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三台机床生产直径为60mm的螺丝,为了检验产品质量,从三台机床生产的螺丝中各抽取了20个测量其直径,进行数据处理后,发现三组数据的平均数都是60mm,它们的方差依次为S甲2=0.612,S乙2=0.058,S丙2=0.149,根据以上提供的信息,你认为生产螺丝的质量最好的是__机床.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F. 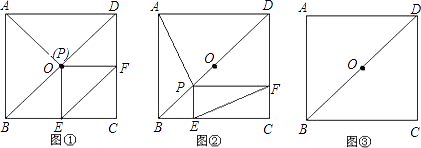
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
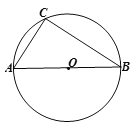
【题目】已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
(1)求⊙O的半径;
(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com