
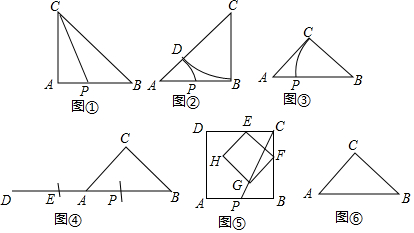
·ÖĪö £Ø1£©ČēĶ¼¢Ł£¬¹żP×÷PD”ĶBCÓŚD£¬øł¾ŻµČŃüČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻB=45”ć£¬ĶĘ³ö”÷PBDŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬µĆµ½PD£ŗPB=1£ŗ$\sqrt{2}$£¬øł¾Ż½ĒĘ½·ÖĻߵĊŌÖŹµĆµ½PA=PD£¬ÓŚŹĒµĆµ½½įĀŪ£»
£Ø2£©¢ŁÓɵČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½AB=BC£¬AC=$\sqrt{2}$AB£¬ÉčAP=AD=x£¬PB=y£¬ĒóµĆ$\frac{x}{y}$=1£¬µĆµ½AP£ŗPB=1£ŗ1£¬ÓŚŹĒµĆµ½ÕāĪ»Ķ¬Ń§µÄ×÷Ķ¼“ķĪó£»
¢Śøł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½AC=BC£¬AB=$\sqrt{2}$BC£¬ÉčAP=x£¬PB=BP=y£¬ŌņAB=x+y£¬µĆµ½AP£ŗPB=$\sqrt{2}$-1£¬ÓŚŹĒµĆµ½ÕāĪ»Ķ¬Ń§µÄ×÷Ķ¼“ķĪó£»
¢Ūøł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½AC=BC=$\frac{\sqrt{2}}{2}$AB£¬ÉčAP=x£¬PB=y£¬µĆµ½$\frac{x}{y}$=$\frac{1}{\sqrt{2}}$£¬ÓŚŹĒµĆµ½ÕāĪ»Ķ¬Ń§µÄ×÷Ķ¼ÕżČ·£»
¢Üøł¾ŻŅŃÖŖĢõ¼žµĆµ½ÉčCE=1£¬CF=$\sqrt{2}$£¬¹żG×÷GH”ĶBCÓŚH£¬ÓŚŹĒµĆµ½FH=CE=1£¬HG=CF=$\sqrt{2}$£¬ÉčPA=x£¬PB=y£¬øł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹµĆµ½$\frac{x}{y}$=$\frac{1}{\sqrt{2}}$£¬ÓŚŹĒµĆµ½ÕāĪ»Ķ¬Ń§µÄ×÷Ķ¼ÕżČ·£»
£Ø3£©×÷”ĻCABµÄ½ĒĘ½·ÖĻßAH½»BCÓŚH£¬¹żH×÷HP”ĪAC½»ABÓŚP£¬ÓŚŹĒµĆµ½AP£ŗPB=1£ŗ$\sqrt{2}$£¬¼“æɵƵ½½įĀŪ£®
½ā“š  ½ā£ŗ£Ø1£©ČēĶ¼¢Ł£¬¹żP×÷PD”ĶBCÓŚD£¬
½ā£ŗ£Ø1£©ČēĶ¼¢Ł£¬¹żP×÷PD”ĶBCÓŚD£¬
”ߣ¬”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻA=90”ć£¬
”ą”ĻB=45”ć£¬
”ą”÷PBDŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąPD£ŗPB=1£ŗ$\sqrt{2}$£¬
”ßCPŹĒ½ĒĘ½·ÖĻߣ¬
”ąPA=PD£¬
”ąPA£ŗPB=1£ŗ$\sqrt{2}$£¬
”ąµćPŹĒABµÄ”°°×Ņų·Öøīµć”±£»
£Ø2£©¢Ł”ß”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻABC=90”ć£¬
”ąAB=BC£¬AC=$\sqrt{2}$AB£¬
ÉčAP=AD=x£¬PB=y£¬
ŌņAB=BC=x+y£¬AC=$\sqrt{2}$£Øx+y£©£¬
”ßAC=AD+CD=AP+BC=2x+y£¬
”ą$\sqrt{2}$£Øx+y£©=2x+y£¬
”ą$\frac{x}{y}$=1£¬
”ąAP£ŗPB=1£ŗ1£¬
”ąÕāĪ»Ķ¬Ń§µÄ×÷Ķ¼“ķĪó£»
¢Ś”ß”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻACB=90”ć£¬
”ąAC=BC£¬AB=$\sqrt{2}$BC£¬
ÉčAP=x£¬PB=BP=y£¬
ŌņAB=x+y£¬
”ąx+y=$\sqrt{2}$
”ąx£ŗy=$\sqrt{2}$-1£¬
”ąAP£ŗPB=$\sqrt{2}$-1£¬
”ąÕāĪ»Ķ¬Ń§µÄ×÷Ķ¼“ķĪó£»
¢Ū”ß”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻC=90”ć£¬
”ąAC=BC=$\frac{\sqrt{2}}{2}$AB£¬
ÉčAP=x£¬PB=y£¬
”ąAD=AB=x+y£¬
”ąPD=2x+y£¬
”ąAC=$\frac{PD}{2}$=$\frac{2x+y}{2}$=$\frac{\sqrt{2}}{2}$£Øx+y£©£¬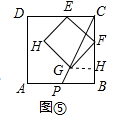
”ą$\frac{x}{y}$=$\frac{1}{\sqrt{2}}$£¬
”ąÕāĪ»Ķ¬Ń§µÄ×÷Ķ¼ÕżČ·£»
¢Ü”ßCE£ŗCF=1£ŗ$\sqrt{2}$£¬
”ąÉčCE=1£¬CF=$\sqrt{2}$£¬
¹żG×÷GH”ĶBCÓŚH£¬
Ōņ”÷CEF”Õ”÷HGF£¬
”ąFH=CE=1£¬HG=CF=$\sqrt{2}$£¬
ÉčPA=x£¬PB=y£¬
”ąBC=AB=x+y£¬
”ßGH”ĪAB£¬
”ą”÷CGH”×”÷CPB£¬
”ą$\frac{HG}{PB}=\frac{CH}{BC}$£¬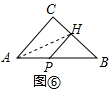
¼“$\frac{\sqrt{2}}{y}=\frac{\sqrt{2}+1}{x+y}$£¬
”ą$\frac{x}{y}$=$\frac{1}{\sqrt{2}}$£¬
”ąÕāĪ»Ķ¬Ń§µÄ×÷Ķ¼ÕżČ·£»
¹Ź“š°øĪŖ£ŗ¢Ū¢Ü£»
£Ø3£©×÷”ĻCABµÄ½ĒĘ½·ÖĻßAH½»BCÓŚH£¬¹żH×÷HP”ĪAC½»ABÓŚP£¬
ŌņAP£ŗPB=1£ŗ$\sqrt{2}$£¬
¼“µćPŹĒABµÄ”°°×Ņų·Öøīµć”±£®
µćĘĄ ±¾Ģāæ¼²éĮĖµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹ£¬Õż·½ŠĪµÄŠŌÖŹ£¬Čż½ĒŠĪ½ĒĘ½·ÖĻߵĊŌÖŹ£¬ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ£¬ÕżČ·µÄĄķ½ā”°°×Ņų·Öøīµć”±ŹĒ½āĢāµÄ¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬½«Čż½Ē°åµÄÖ±½Ē¶„µć·ÅŌŚÖ±³ßµÄŅ»±ßÉĻ£¬”Ļ1=30”ć£¬”Ļ2=70”ć£¬Ōņ”Ļ3=50”ć£®
ČēĶ¼£¬½«Čż½Ē°åµÄÖ±½Ē¶„µć·ÅŌŚÖ±³ßµÄŅ»±ßÉĻ£¬”Ļ1=30”ć£¬”Ļ2=70”ć£¬Ōņ”Ļ3=50”ć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
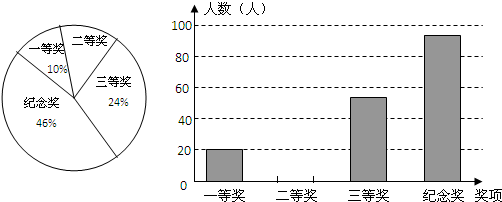
 ČēĶ¼£¬ĪŖ³½üĀ·¼łĢ¤²ŻĘŗŹĒŅ»ÖÖ²»ĪÄĆ÷ĻÖĻó£¬ĒėÄćÓĆŹżŃ§ÖŖŹ¶½āŹĶ³öĻÖÕāŅ»ĻÖĻóµÄŌŅņŹĒ£Ø””””£©
ČēĶ¼£¬ĪŖ³½üĀ·¼łĢ¤²ŻĘŗŹĒŅ»ÖÖ²»ĪÄĆ÷ĻÖĻó£¬ĒėÄćÓĆŹżŃ§ÖŖŹ¶½āŹĶ³öĻÖÕāŅ»ĻÖĻóµÄŌŅņŹĒ£Ø””””£©| A£® | Į½µćČ·¶ØŅ»ĢõÖ±Ļß | B£® | Į½µćÖ®¼ä£¬Ļ߶Ī×ī¶Ģ | ||
| C£® | Ö±Ļß±ČĻ߶Ī¶Ģ | D£® | Ķ¬½Ē£ØµČ½Ē£©µÄÓą½ĒĻąµČ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
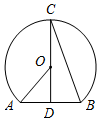 ČēĶ¼ĖłŹ¾£¬µćDŹĒĻŅABµÄÖŠµć£¬µćCŌŚ”ŃOÉĻ£¬CD¾¹żŌ²ŠÄO£¬ŌņĻĀĮŠ½įĀŪÖŠ²»Ņ»¶ØÕżČ·µÄŹĒ£Ø””””£©
ČēĶ¼ĖłŹ¾£¬µćDŹĒĻŅABµÄÖŠµć£¬µćCŌŚ”ŃOÉĻ£¬CD¾¹żŌ²ŠÄO£¬ŌņĻĀĮŠ½įĀŪÖŠ²»Ņ»¶ØÕżČ·µÄŹĒ£Ø””””£©| A£® | CD”ĶAB | B£® | ”ĻOAD=2”ĻCBD | C£® | ”ĻAOD=2”ĻBCD | D£® | »”AC=»”BC |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
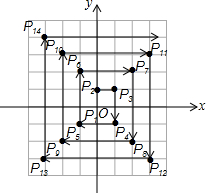 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ćæøö×īŠ”·½øńµÄ±ß³¤¾łĪŖ1øöµ„Ī»³¤£¬P1£¬P2£¬P3£¬”£¬¾łŌŚøńµćÉĻ£¬ĘäĖ³Šņ°“Ķ¼ÖŠ”°”ś”±·½ĻņÅÅĮŠ£¬Čē£ŗP1£Ø0£¬0£©£¬P2£Ø0£¬1£©£¬P3£Ø1£¬1£©£¬P4£Ø1£¬-1£©£¬P5£Ø-1£¬-1£©£¬P6£Ø-1£¬2£©”øł¾ŻÕāøö¹ęĀÉ£¬µćP2017µÄ×ų±źĪŖ£Ø-504£¬-504£©£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ćæøö×īŠ”·½øńµÄ±ß³¤¾łĪŖ1øöµ„Ī»³¤£¬P1£¬P2£¬P3£¬”£¬¾łŌŚøńµćÉĻ£¬ĘäĖ³Šņ°“Ķ¼ÖŠ”°”ś”±·½ĻņÅÅĮŠ£¬Čē£ŗP1£Ø0£¬0£©£¬P2£Ø0£¬1£©£¬P3£Ø1£¬1£©£¬P4£Ø1£¬-1£©£¬P5£Ø-1£¬-1£©£¬P6£Ø-1£¬2£©”øł¾ŻÕāøö¹ęĀÉ£¬µćP2017µÄ×ų±źĪŖ£Ø-504£¬-504£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com