【题目】如图，二次函数y＝x（x﹣3）（0≤x≤3）的图象，记为C1，它与x轴交于点O，A1；将C1点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；……若P（2020，m）在这个图象连续旋转后的所得图象上，则m＝_____．
【答案】2．
【解析】
x（x﹣3）＝0得A1（3，0），再根据旋转的性质得OA1＝A1A2＝A2A3＝…＝A673A674＝3，所以抛物线C764的解析式为y＝﹣（x﹣2019）（x﹣2022），然后计算自变量为2020对应的函数值即可．
当y＝0时，x（x﹣3）＝0，解得x1＝0，x2＝3，则A1（3，0），
∵将C1点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；……
∴OA1＝A1A2＝A2A3＝…＝A673A674＝3，
∴抛物线C764的解析式为y＝﹣（x﹣2019）（x﹣2022），
把P（2020，m）代入得m＝﹣（2020﹣2019）（2020﹣2022）＝2．
故答案为2．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，一次函数
的图象分别交x轴、y轴于C，D两点，交反比例函数
图象于A（
，4），B（3，m）两点.
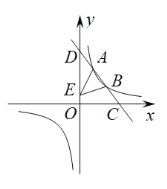
(1)求直线CD的表达式；
(2)点E是线段OD上一点，若
，求E点的坐标；
(3)请你根据图象直接写出不等式
的解集.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的口袋中装有4张卡片，卡片上分别标有数字1、－2、－3、4，它们除了标有的数字不同之外再也没有其它区别，小芳从盒子中随机抽取一张卡片．
（1）求小芳抽到负数的概率；
（2）若小明再从剩余的三张卡片中随机抽取一张，请你用树状图或列表法，求小明和小芳两人均抽到负数的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
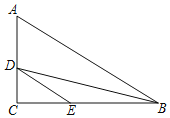
【题目】如图，△ABC中，∠C＝90°，∠B＝30°，AC＝
，D、E分别在边AC、BC上，CD＝1，DE∥AB，将△CDE绕点C旋转，旋转后点D、E对应的点分别为D′、E′，当点E′落在线段AD′上时，连接BE′，此时BE′的长为（ ）
A.2
B.3C.2D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，顶点为P（2，﹣4）的二次函数y＝ax2+bx+c的图象经过原点，点A（m，n）在该函数图象上，连接AP、OP．
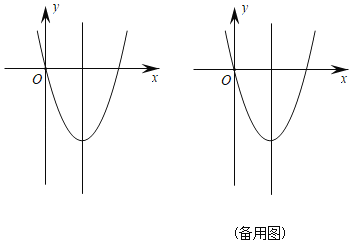
（1）求二次函数y＝ax2+bx+c的表达式；
（2）若∠APO＝90°，求点A的坐标；
（3）若点A关于抛物线的对称轴的对称点为C，点A关于y轴的对称点为D，设抛物线与x轴的另一交点为B，请解答下列问题：
①当m≠4时，试判断四边形OBCD的形状并说明理由；
②当n＜0时，若四边形OBCD的面积为12，求点A的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
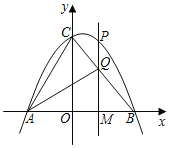
【题目】如图，抛物线y＝﹣
x2+bx+c交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．
（1）求此抛物线的表达式；
（2）求过B、C两点的直线的函数表达式；
（3）点P是第一象限内抛物线上的一个动点．过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点P的坐标，若不存在，请说明理由；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，点C，D为
上的点，且
＝
，延长AD，BC相交于点E，连接OD交AC于点F．
（1）求证：△ABC≌△AEC；
（2）若OA＝3，BC＝4，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
的对称轴是直线
，且与
轴相交于A，B两点（点B在点A的右侧），与
轴交于点C．
（1）求抛物线的解析式和A，B两点的坐标；
（2）若点P是抛物线上B、C两点之间的一个动点（不与B,C重合），则是否存在一点P，使△BPC的面积最大？若存在，请求出△BPC的最大面积；若不存在，试说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“铁路建设助推经济发展”，近年来我国政府十分重视铁路建设.渝利铁路通车后，从重庆到上海比原铁路全程缩短了320千米，列车设计运行时速比原铁路设计运行时速提高了120千米/小时，全程设计运行时间只需8小时，比原铁路设计运行时间少用16小时.
（1）渝利铁路通车后，重庆到上海的列车设计运行里程是多少千米?
（2）专家建议：从安全的角度考虑,实际运行时速要比设计时速减少m%，以便于有充分时间应对突发事件，这样，从重庆到上海的实际运行时间将增加
小时，求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com