
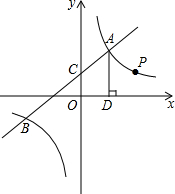
 ��ͼ��һ�κ���y1=k1x+b �뷴��������y2=$\frac{{k}_{2}}{x}$ ��ͼ���ڵ�A��2��m����B��-6��-2������y�ύ�ڵ�C��
��ͼ��һ�κ���y1=k1x+b �뷴��������y2=$\frac{{k}_{2}}{x}$ ��ͼ���ڵ�A��2��m����B��-6��-2������y�ύ�ڵ�C������ ��1���ɵ�B���������ô���ϵ�������������������������ʽ���ɵ�A�ڷ���������ͼ���Ͻ�ϵ�A�ĺ����꼴�ɵó���A�����꣬���ɵ�A��B���������ô���ϵ�����������һ�κ�������ʽ��
��2������������ͼ�������λ�ù�ϵ�������ҳ�����ʽ�Ľ⣻
��3������BD���ɵ�A����������D������꣬�������ľ��빫ʽ�������AD��AB��BD�ij��ȣ��Ӷ��������ABD���ܳ����ٸ��������ε������ʽ���������ABD�������
��4������O����һ�����Ľ�ƽ����l������AP��ֱ��l�ڵ�Q����ʱPQ+AQ��̣�����OP=5�Լ���P�ڷ���������ͼ���ϼ��������P�����꣬�ɵ�A��P���������ô���ϵ�����������ֱ��AP�Ľ���ʽ������ֱ��AP��l����ʽ�ɷ����飬�ⷽ���鼴�ɵó����ۣ�
��� �⣺��1���ߵ�B��-6��-2���ڷ���������y2=$\frac{{k}_{2}}{x}$ ��ͼ���ϣ�
��-2=$\frac{{k}_{2}}{-6}$����ã�k2=12��
�෴������������ʽΪy2=$\frac{12}{x}$��
�ߵ�A��2��m���ڷ���������y2=$\frac{12}{x}$��ͼ���ϣ�
��m=$\frac{12}{2}$=6����A��2��6����
��A��2��6����B��-6��-2������y1=k1x+b��
��$\left\{\begin{array}{l}{2{k}_{1}+b=6}\\{-6{k}_{1}+b=-2}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{k}_{1}=1}\\{b=4}\end{array}\right.$��
��һ�κ���y1=x+4��
�ʴ�Ϊ��x+4��$\frac{12}{x}$��
��2���۲캯��ͼ���֣�
��x��-6��0��x��2ʱ��һ�κ���ͼ���ڷ���������ͼ����·���
�൱ y1��y2ʱ��x��ȡֵ��Χ��x��-6��0��x��2��
�ʴ�Ϊ��x��-6��0��x��2��
��3������BD����ͼ1��ʾ��
�ߵ�A��2��6����
���D��2��0����
��AB=8$\sqrt{2}$��AD=6��BD=2$\sqrt{17}$��
��C��ABD=AB+BD+AD=8$\sqrt{2}$+2$\sqrt{17}$+6��
S��ABD=$\frac{1}{2}$AD•��xA-xB��=$\frac{1}{2}$��6��[2-��-6��]=24��
��4������O����һ�����Ľ�ƽ����l������AP��ֱ��l�ڵ�Q����ʱPQ+AQ��̣���ͼ2��ʾ��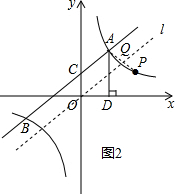
��ֱ��lΪ��һ�����Ľ�ƽ���ߣ�
��ֱ��l�Ľ���ʽΪy=x��
���P��������m��n����0��n��m����
�ߵ�P�ڷ���������y2=$\frac{12}{x}$��ͼ���ϣ���OP=5��
��$\left\{\begin{array}{l}{mn=12}\\{{m}^{2}+{n}^{2}=25}\end{array}\right.$����ã�$\left\{\begin{array}{l}{m=4}\\{n=3}\end{array}\right.$����$\left\{\begin{array}{l}{m=3}\\{n=4}\end{array}\right.$����ȥ������$\left\{\begin{array}{l}{m=-4}\\{n=-3}\end{array}\right.$����ȥ������$\left\{\begin{array}{l}{m=-3}\\{n=-4}\end{array}\right.$����ȥ����
���P��4��3����
��ֱ��AP�Ľ���ʽΪy=ax+c��
����$\left\{\begin{array}{l}{6=2a+c}\\{3=4a+c}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{c=9}\end{array}\right.$��
��ֱ��AP�Ľ���ʽΪy=-$\frac{3}{2}$x+9��
����ֱ��AP��l�Ľ���ʽ�ã�$\left\{\begin{array}{l}{y=-\frac{3}{2}x+9}\\{y=x}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=\frac{18}{5}}\\{y=\frac{18}{5}}\end{array}\right.$��
�ʵ�Q������Ϊ��$\frac{18}{5}$��$\frac{18}{5}$����
���� ���⿼���˴���ϵ������������ʽ�������ε����Լ��ܳ�������Ĺؼ��ǣ���1�����ô���ϵ���������������ʽ����2�����ݺ���ͼ�������λ�ù�ϵ�������ʽ����3������߶�AD��AB��BD�ij��ȣ���4���ҳ���Q��λ�ã����������е��⣬�ѶȲ����Ϸ����������������Ŀʱ���ҳ�������꣬���ô���ϵ���������������ʽ�ǹؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
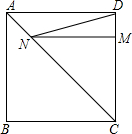 ��ͼ��ʾ��������ABCD�ı߳�Ϊ4����M�ڱ�DC�ϣ���DM=1����N�DZ�AC��һ���㣬���߶�DN+MN����СֵΪ��������
��ͼ��ʾ��������ABCD�ı߳�Ϊ4����M�ڱ�DC�ϣ���DM=1����N�DZ�AC��һ���㣬���߶�DN+MN����СֵΪ��������| A�� | 4 | B�� | 4$\sqrt{2}$ | C�� | 2$\sqrt{17}$ | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{12}-\sqrt{3}=\sqrt{3}$ | B�� | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C�� | $3\sqrt{5}-\sqrt{5}=3$ | D�� | $3+2\sqrt{2}=5\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�����OABC�ı�OA��OC�ֱ���x���y���ϣ�OC=3��OA=2$\sqrt{6}$��D��BC���е㣬����OCD��ֱ��OD�۵���õ���OGD���ӳ�OG��AB�ڵ�E������DE�����G������Ϊ��$\frac{6\sqrt{6}}{5}$��$\frac{3}{5}$����
��ͼ����ƽ��ֱ������ϵxOy�У�����OABC�ı�OA��OC�ֱ���x���y���ϣ�OC=3��OA=2$\sqrt{6}$��D��BC���е㣬����OCD��ֱ��OD�۵���õ���OGD���ӳ�OG��AB�ڵ�E������DE�����G������Ϊ��$\frac{6\sqrt{6}}{5}$��$\frac{3}{5}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ı��� | B�� | ���������� | C�� | ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com