
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位:km):
第一次 | 第二次 | 第三次 | 第四次 |
x |
| x﹣5 | 2(6﹣x) |
(1)写出这辆出租车每次行驶的方向;
(2)求经过连续4次行驶后,这辆出租车所在的位置(结果可用x表示);
(3)这辆出租车一共行驶了多少路程(结果用x表示)?
【答案】(1)第一次是向东,第二次是向西,第三次是向东,第四次是向西;(2)这辆出租车所在的位置是向东(7﹣![]() )km;(3)这辆出租车一共行驶了(
)km;(3)这辆出租车一共行驶了(![]() )km的路程.
)km的路程.
【解析】
(1)以A为原点,根据数的符号即可判断车的行驶方向;
(2)将四次行驶路程(包括方向)相加,根据判断出租车的位置;
(3)将四次行驶路程的绝对值相加即可.
(1)解:第一次是向东,第二次是向西,第三次是向东,第四次是向西;
(2)x+(-![]() )+(x﹣5)+2(6﹣x)=7﹣
)+(x﹣5)+2(6﹣x)=7﹣![]()
∵x>6且x<14,
∴7﹣![]() >0
>0
∴经过连续4次行驶后,这辆出租车所在的位置是向东(7﹣![]() )km.
)km.
(3):|x|+|-![]() |+|x﹣5|+|2(6﹣x)|=
|+|x﹣5|+|2(6﹣x)|=![]() .
.
答:这辆出租车一共行驶了(![]() )km的路程.
)km的路程.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系(一次函数)配套设计的,下表列出5套符合条件的课桌椅的高度. ①假设课桌的高度为ycm椅子的高度为xcm,请确定y与x的函数关系式;②现有一把高37cm的椅子和一张高71.5cm的课桌,它们是否配套?为什么?
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点P的坐标为(m+1,m﹣1).
(1)试判断点P是否在一次函数y=x﹣2的图象上,并说明理由;
(2)如图,一次函数y=﹣ ![]() x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.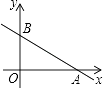
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图①,图形l外一点P与图形l上各点连接的所有线段中,若线段PA1最短,则线段PA1的长度称为点P到图形l的距离.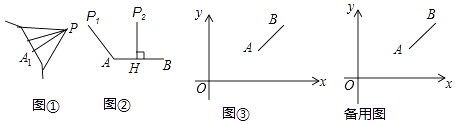
例如:图②中,线段P1A的长度是点P1到线段AB的距离;线段P2H的长度是点P2到线段AB的距离.
解决问题:
如图③,平面直角坐标系xOy中,点A、B的坐标分别为(8,4),(12,7),点P从原点O出发,以每秒1个单位长度的速度向x轴正方向运动了t秒.
(1)当t=4时,求点P到线段AB的距离;
(2)t为何值时,点P到线段AB的距离为5?
(3)t满足什么条件时,点P到线段AB的距离不超过6?(直接写出此小题的结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
A.5 ![]()
B.10 ![]()
C.10 ![]()
D.15 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )
A.16
B.16 ![]()
C.20
D.20 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)若∠AOE=32°,求∠BOC的度数;
(2)若OD是∠AOC的角平分线,求∠AOE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com