
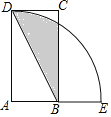
【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
科目:初中数学 来源: 题型:
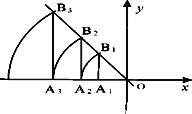
【题目】如图,直线l:y=-![]() x,点A1坐标为(-4,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2018的坐标为_______.
x,点A1坐标为(-4,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2018的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
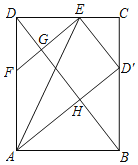
【题目】如图,在矩形ABCD中,E为CD上一点,若△ADE沿直线AE翻折,使点D落在BC边上点D′处.F为AD上一点,且DF=CD',EF与BD相交于点G,AD′与BD相交于点H.D′E∥BD,HG=4,则BD=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
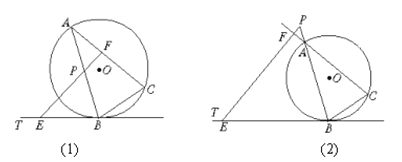
【题目】已知:△ABC是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过P作BC的平行线交直线BT于点E,交直线AC于点F.
(1)如图 (1)所示,当P在线段AB上时,求证:PA·PB=PE·PF;
(2)如图 (2)所示,当P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 是边
是边![]() 上一点(不与点
上一点(不与点![]() 重合),点
重合),点![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() .
.
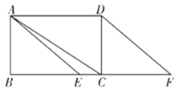
(1)求证:![]()
(2)连接![]() ,其中
,其中![]()
①当四边形![]() 是菱形时,求线段
是菱形时,求线段![]() 与线段
与线段![]() 之间的距离;
之间的距离;
②若点![]() 是
是![]() 的内心,连接
的内心,连接![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店经销进价分别为![]() 元/千克、
元/千克、![]() 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
时间 | 甲水果销量 | 乙水果销量 | 销售收入 |
周五 |
|
|
|
周六 |
|
|
|
(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于![]() 元的资金再购进两种水果共
元的资金再购进两种水果共![]() 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?
(3)在(2)的条件下,水果店销售完这![]() 千克水果能否实现利润为
千克水果能否实现利润为![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
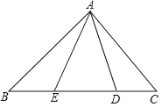
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=_____(用含a、b的式子表示AB).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图l、图2均为8×6的方格纸(每个小正方形的边长均为1),在方格纸中各有一条线段AB,其中点A、B均在小正方形的顶点上,请按要求画图:

(1)在图l中画一直角△ABC,使得tan∠BAC=![]() ,点C在小正方形的顶点上;
,点C在小正方形的顶点上;
(2)在图2中画一个□ABEF,使得□ABEF的面积为图1中△ABC面积的4倍,点E、F在小正方形的顶点上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com