
Ζ÷Έω Θ®1Θ© Ήœ»…ηΒψMΒΡΉχ±ξ «Θ®xΘ§yΘ©Θ§‘ρ‘Ύ±δΜΜTΒΡΉς”Οœ¬Θ§ΒψMΘ®xΘ§yΘ©±Μ±δΈΣΒψMΓδΘ®2x-yΘ§3x-2y+3Θ©Θ§»ΜΚσΗυΨίΒψMΓδΒΡΉχ±ξ «Θ®1Θ§-1Θ©Θ§Ν–≥ωΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΉιΘ§«σ≥ωxΓΔyΒΡ÷ΒΘ§Φ¥Ω…«σ≥ωΒψMΒΡΉχ±ξΘ°
Θ®2Θ© Ήœ»«σ≥ωΒψNΘ®$\frac{m}{4}$Θ§mΘ©‘Ύ±δΜΜTΒΡΉς”Οœ¬ΒΡΒψNΓδΒΡΉχ±ξ «Εύ…ΌΘΜ»ΜΚσΗυΨίΒψNΓδ‘ΎΒΎΕΰœσœόΘ§Ω…ΒΟΒψNΓδΒΡΚαΉχ±ξ–Γ”Ύ0Θ§ΉίΉχ±ξ¥σ”Ύ0Θ§«σ≥ω Β ΐmΒΡ»Γ÷ΒΖΕΈßΦ¥Ω…Θ°
Θ®3Θ©ΔΌΒ±x=y ±Θ§≤Μ¥φ‘Ύ“Μ¥ΈΚ· ΐy=kx+bΘ§ ΙΒΟΒψQΚΆQΓδΕΦ‘Ύ’βΗω“Μ¥ΈΚ· ΐΒΡΆΦœσ…œΘΜΔΎΒ±xΓΌy ±Θ§¥φ‘Ύ“Μ¥ΈΚ· ΐy=kx+bΘ§ ΙΒΟΒψQΚΆQΓδΕΦ‘Ύ’βΗω“Μ¥ΈΚ· ΐΒΡΆΦœσ…œΘ§ΗυΨίΒψQΚΆQΓδΕΦ‘Ύ“Μ¥ΈΚ· ΐy=kx+bΒΡΆΦœσ…œΘ§Ν–≥ωΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΉιΘ§«σ≥ωkΓΔbΒΡ÷ΒΗς «Εύ…ΌΦ¥Ω…Θ°
Ϋβ¥π ΫβΘΚΘ®1Θ©…ηΒψMΒΡΉχ±ξ «Θ®xΘ§yΘ©Θ§
‘ρ‘Ύ±δΜΜTΒΡΉς”Οœ¬Θ§ΒψMΘ®xΘ§yΘ©±Μ±δΈΣΒψMΓδΘ®2x-yΘ§3x-2y+3Θ©Θ§
Γύ$\left\{\begin{array}{l}{2x-y=1}\\{3x-2y+3=-1}\end{array}\right.$
ΫβΒΟ$\left\{\begin{array}{l}{x=6}\\{y=11}\end{array}\right.$
ΓύΒψMΒΡΉχ±ξ «Θ®6Θ§11Θ©Θ°
Θ®2Θ©2x-y=2ΓΝ$\frac{m}{4}$-m=$\frac{m}{2}-m=-\frac{m}{2}$
3x-2y+3=3ΓΝ$\frac{m}{4}$-2m+3=$\frac{3}{4}m$-2m+3=-$\frac{5}{4}m+3$
ΓΏΒψNΓδ‘ΎΒΎΕΰœσœόΘ§
Γύ$\left\{\begin{array}{l}{-\frac{m}{2}ΘΦ0}\\{-\frac{5}{4}m+3ΘΨ0}\end{array}\right.$
ΫβΒΟ0ΘΦmΘΦ2.4Θ§
Φ¥ Β ΐmΒΡ»Γ÷ΒΖΕΈß «0ΘΦmΘΦ2.4Θ°
Θ®3Θ©ΔΌΒ±x=y ±Θ§≤Μ¥φ‘Ύ“Μ¥ΈΚ· ΐy=kx+bΘ§ ΙΒΟΒψQΚΆQΓδΕΦ‘Ύ’βΗω“Μ¥ΈΚ· ΐΒΡΆΦœσ…œΘ°
ΔΎΒ±xΓΌy ±Θ§¥φ‘Ύ“Μ¥ΈΚ· ΐy=kx+bΘ§ ΙΒΟΒψQΚΆQΓδΕΦ‘Ύ’βΗω“Μ¥ΈΚ· ΐΒΡΆΦœσ…œΘ°
ΔΌΒ±x=y ±Θ§
ΓΏΒψQΘ®xΘ§xΘ©‘Ύ±δΜΜTΒΡΉς”Οœ¬Ε‘”ΠΒψΈΣQΓδΘ®xΘ§x+3Θ©Θ§
Γύ≤Μ¥φ‘Ύ“Μ¥ΈΚ· ΐy=kx+bΘ§ ΙΒΟΒψQΚΆQΓδΕΦ‘Ύ’βΗω“Μ¥ΈΚ· ΐΒΡΆΦœσ…œΘ°
ΔΎΒ±xΓΌy ±Θ§ΒψQΘ®xΘ§yΘ©‘Ύ±δΜΜTΒΡΉς”Οœ¬Ε‘”ΠΒψΈΣQΓδΘ®2x-yΘ§3x-2y+3Θ©Θ§
ΓΏΒψQΚΆQΓδΕΦ‘Ύ“Μ¥ΈΚ· ΐy=kx+bΒΡΆΦœσ…œΘ§
Γύ$\left\{\begin{array}{l}{y=kx+b}\\{3x-2y+3=kΘ®2x-yΘ©+b}\end{array}\right.$
ΫβΒΟ$\left\{\begin{array}{l}{k=3-\frac{3}{y-x}}\\{b=y-3x+\frac{3x}{y-x}}\end{array}\right.$
ΓύΒ±xΓΌy ±Θ§¥φ‘Ύ“Μ¥ΈΚ· ΐy=kx+bΘ§ ΙΒΟΒψQΚΆQΓδΕΦ‘Ύ’βΗω“Μ¥ΈΚ· ΐΒΡΆΦœσ…œΘ§¥Υ ±k=3-$\frac{3}{y-x}$Θ§b=y-3x+$\frac{3x}{y-x}$Θ°
ΒψΤά Θ®1Θ©¥ΥΧβ÷ς“ΣΩΦ≤ιΝΥ“Μ¥ΈΚ· ΐΉέΚœΧβΘ§ΩΦ≤ιΝΥΖ÷ΈωΆΤάμΡήΝΠΘ§ΩΦ≤ιΝΥΖ÷άύΧ÷¬έΥΦœκΒΡ”Π”ΟΘ§ΩΦ≤ιΝΥ¥”“―÷ΣΚ· ΐΆΦœσ÷–Μώ»Γ–≈œΔΘ§≤ΔΡήάϊ”ΟΜώ»ΓΒΡ–≈œΔΫβ¥πœύ”ΠΒΡΈ ΧβΒΡΡήΝΠΘ°
Θ®2Θ©¥ΥΧβΜΙΩΦ≤ιΝΥΗςΗωœσœόΒΡΒψΒΡΧΊ’ςΘ§“‘ΦΑΦΗΚΈ±δΜΜΒΡ÷Σ ΕΘ§“Σ λΝΖ’ΤΈ’Θ°


 ΤΎΡ©±ΠΒδΒΞ‘ΣΦλ≤βΖ÷άύΗ¥œΑΨμœΒΝ–¥πΑΗ
ΤΎΡ©±ΠΒδΒΞ‘ΣΦλ≤βΖ÷άύΗ¥œΑΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 7 | BΘ° | 8 | CΘ° | 9 | DΘ° | 18 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
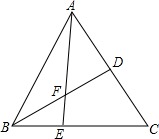 »γΆΦΘ§‘ΎΓςABC÷–Θ§E «BC±Ώ…œΒΡ“ΜΒψΘ§EC=2BEΘ§ΒψD «ABΒΡ÷–ΒψΘ§«“SΓςABC=18Θ§‘ρSΥΡ±Ώ–ΈCDFEΒΡΟφΜΐΘΩ
»γΆΦΘ§‘ΎΓςABC÷–Θ§E «BC±Ώ…œΒΡ“ΜΒψΘ§EC=2BEΘ§ΒψD «ABΒΡ÷–ΒψΘ§«“SΓςABC=18Θ§‘ρSΥΡ±Ώ–ΈCDFEΒΡΟφΜΐΘΩ≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
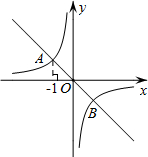 “―÷ΣΘΚ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§“Μ¥ΈΚ· ΐy=-xΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐy=-$\frac{1}{x}$ΒΡΆΦœσΫΜ”ΎAΓΔBΝΫΒψΘ°
“―÷ΣΘΚ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§“Μ¥ΈΚ· ΐy=-xΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐy=-$\frac{1}{x}$ΒΡΆΦœσΫΜ”ΎAΓΔBΝΫΒψΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com