
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧 上有一点E使∠EBC=∠DEC,延长BE依次交AC于G,交⊙O于H.
上有一点E使∠EBC=∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CG和CE的长.
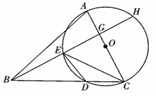

证明:⑴连接AD
∵∠DAC=∠DEC ∠EBC=∠DEC ∴∠DAC=∠EBC
又∵AC是⊙O的直径 ∴∠ADC=90° ∴∠DCA+∠DAC=90°
∴∠EBC+∠DCA=90° ∴∠BGC=180°-(∠EBC+∠DCA)=180°-90°=90°
∴AC⊥BH
⑵∵∠BDA=180°-∠ADC=90°∠ABC=45°
∴∠BAD=45° ∴BD=AD
∵BD=8 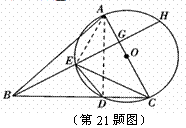

∴AD=8
又∵∠ADC=90° AC=10 ∴由勾股定理,得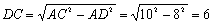 .
.
∴BC=BD+DC=8+6=14
又∵∠BGC=∠ADC=90° ∠BCG=∠ACD
∴△BCG∽△ACD ∴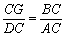 ∴
∴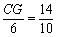 ∴
∴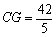
连结AE,∵AC是直径 ∴∠AEC=90°
又∵EG⊥AC
∴△CEG∽△CAE ∴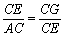 ∴
∴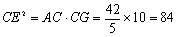
∴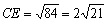 .
.


科目:初中数学 来源: 题型:
已知二次函数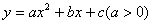 经过点M(-1,2)和点N(1,-2),交x轴于
经过点M(-1,2)和点N(1,-2),交x轴于
A,B两点,交y轴于C则( ).
①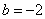 ;
;
②该二次函数图像与y轴交于负半轴
③ 存在这样一个a,使得M、A、C三点在同一条直线上
④若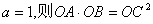
以上说法正确的有:
A.①②③④ B. ①②④ C.②③④ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
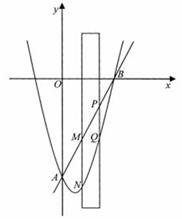
如图,抛物线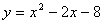 交
交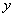 轴于点A,交
轴于点A,交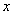 轴正半轴于点B.
轴正半轴于点B.
(1)求直线AB对应的函数关系式;
(2)有一宽度为1的直尺平行于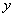 轴;在点A、B之间平行移动;直尺两边长所在直线被直线AB和抛物线截得两线段MN、PQ.设M点的横坐标为
轴;在点A、B之间平行移动;直尺两边长所在直线被直线AB和抛物线截得两线段MN、PQ.设M点的横坐标为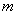 ;且
;且 .试比较线段MN与PQ的大小.
.试比较线段MN与PQ的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com