
【题目】关于x的一元二次方程mx2+3x+1=0有两个不相等的实数根,则m的取值范围为( )
A. m<![]() B. m<
B. m<![]() 且m≠0C. m≤
且m≠0C. m≤![]() D. m≤
D. m≤![]() 且m≠0
且m≠0
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图一,抛物线![]() 过
过![]() 三点
三点
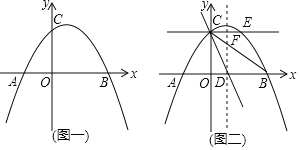
(1)求该抛物线的解析式;
(2)![]() 两点均在该抛物线上,若
两点均在该抛物线上,若![]() ,求
,求![]() 点横坐标
点横坐标![]() 的取值范围;
的取值范围;
(3)如图二,过点![]() 作
作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,该抛物线的对称轴与
,该抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,连结
,连结![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 分别为直线
分别为直线![]() 和
和![]() 上的动点,求
上的动点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3![]() 米.求点B到地面的垂直距离BC.
米.求点B到地面的垂直距离BC.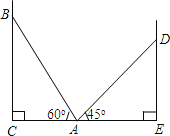
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知有一条抛物线的形状(开口方向和开口大小)与抛物线y=2x![]() 相同,它的对称轴是直线x=2;且当x=1时,y=6,求这条抛物线的解析式。
相同,它的对称轴是直线x=2;且当x=1时,y=6,求这条抛物线的解析式。
(2)定义:如果点P(t,t)在抛物线上,则点P叫做这条抛物线的不动点。
①求出(1)中所求抛物线的所有不动点的坐标;
②当a、b、c满足什么关系式时,抛物线y=ax![]() +bx+c上一定存在不动点。
+bx+c上一定存在不动点。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为10cm的正方形ABCD中,E为AB的中点,连接CE,过点D作![]() 于点
于点![]() ,连接AF,过点E作
,连接AF,过点E作![]() 于点H且交CD的延长线于点
于点H且交CD的延长线于点![]() ,交AD于点
,交AD于点![]() ,连接FG,则
,连接FG,则![]() =_____cm2.
=_____cm2.
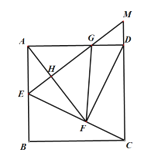
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金堂三溪镇被中国柑桔研究所誉为“中国脐橙第一乡”,2016年12月某公司到三溪镇以2.5元/千克购得脐橙12000千克,这些脐橙的销售期最多还有60天,60天后库存的脐橙不能再销售,需要当垃圾处理,处理费为0.1元/千克,经测算,脐橙的销售价格定为8元/千克时,每天可售出100千克;销售单价每降低0.5元,每天可多售出50千克.
(1).如果按8元/千克的价格销售,能否在60天内售完?这些脐橙按此价格销售,获得的利润是多少?
(2).如果按6元/千克的价格销售,这些脐橙获得的利润是多少?当这些脐橙销售价格定为x(![]() )元/千克时,可以使公司每天获得利润最大,每天的最大利润为多少?
)元/千克时,可以使公司每天获得利润最大,每天的最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点![]() .甲从中山路上点
.甲从中山路上点![]() 出发,骑车向北匀速直行;与此同时,乙从点
出发,骑车向北匀速直行;与此同时,乙从点![]() 出发,沿北京路步行向东匀速直行.设出发
出发,沿北京路步行向东匀速直行.设出发![]() 时,甲、乙两人与点
时,甲、乙两人与点![]() 的距离分别为
的距离分别为![]() 、
、![]() .已知
.已知![]() 、
、![]() 与
与![]() 之间的函数关系如图②所示.
之间的函数关系如图②所示.
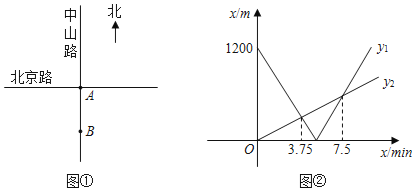
(1)求甲、乙两人的速度;
(2)当![]() 取何值时,甲、乙两人之间的距离最短?
取何值时,甲、乙两人之间的距离最短?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com