
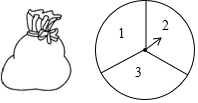
 一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.
一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.分析 (1)画树状图展示所有12种等可能性结果,再找出其中数字之和小于4的结果数,然后根据概率公式求解;
(2)利用概率公式计算出P(和不小于4),则P(和小于4)≠P(和不小于4),于是可判断游戏不公平,改变游戏规则后使数字之和小于4和数字之和不小于4的结果数相等即可.
解答 解:(1)画树状图: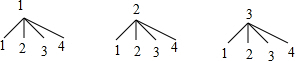
共有12种等可能性结果,其中数字之和小于4的有3种情况,
所以P(和小于4)=$\frac{3}{12}$=$\frac{1}{4}$,
即小颖参加比赛的概率为$\frac{1}{4}$;
(2)该游戏不公平.理由如下:
因为P(和不小于4)=$\frac{3}{4}$,
所以P(和小于4)≠P(和不小于4),
所以游戏不公平,可改为:若数字之和为偶数,则小颖去;若数字之和为奇数,则小亮去.
点评 本题考查了游戏公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.也考查了列表法与树状图法.


科目:初中数学 来源: 题型:解答题
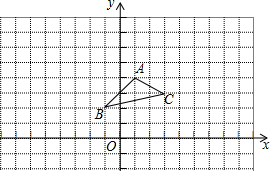 如图,在平面直角坐标系中,△ABC中的三个顶点坐标分别为A(1,4)、B(-1,2)、C(3,3).在x轴上方,请画出以原点O为位似中心,相似比为2:1.将△ABC放大后得到的△A1B1C1,并写出△A1B1C1各顶点的坐标.
如图,在平面直角坐标系中,△ABC中的三个顶点坐标分别为A(1,4)、B(-1,2)、C(3,3).在x轴上方,请画出以原点O为位似中心,相似比为2:1.将△ABC放大后得到的△A1B1C1,并写出△A1B1C1各顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿线段OC-弧CD-线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿线段OC-弧CD-线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )| A. | 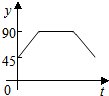 | B. | 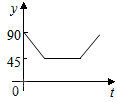 | C. | 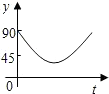 | D. | 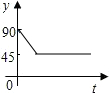 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com