
分析 (1)分别令x=0、y=0求出函数的图象与x轴、y轴的交点坐标,然后根据三角形面积公式求出以此三点为顶点的三角形面积;
(2)画出函数图象,根据图象回答问题即可.
解答 解:(1)令x=0,则y=-6,
∴函数的图象与y轴的交点坐标为(0,-6),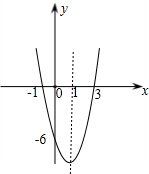
令y=0,则2x2-4x-6=0,
解方程得:x1=-1,x2=3,
∴函数的图象与x轴的交点坐标为(-1,0)(3,0),
∴以此三点为顶点的三角形面积=$\frac{1}{2}$×4×6=12;
(2)画出函数图象,如图,根据图象可以看出,
当x<-1或x>3时,y>0,
当-1<x<3时,y<0.
点评 此题考查了二次函数的性质与图象以及抛物线与坐标轴的交点坐标;熟练运用数形结合思想是解决第二小题的关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:选择题
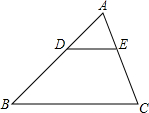 如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )
如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )| A. | 1:2 | B. | 1:4 | C. | 1:25 | D. | $\sqrt{5}$:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
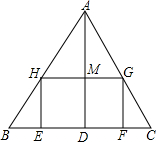 如图,△ABC,是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC,AB上,AD与HG的交点为M.
如图,△ABC,是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC,AB上,AD与HG的交点为M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上,若AD=4,BE=1,求:
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上,若AD=4,BE=1,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
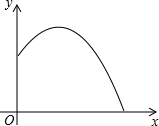 如图是某运动员打羽毛球的抛物线示意图,已知打出羽毛球的高度y(m)与水平距离x(m)之间的函数关系式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+7,则该羽毛球落地时距离发出点( )
如图是某运动员打羽毛球的抛物线示意图,已知打出羽毛球的高度y(m)与水平距离x(m)之间的函数关系式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+7,则该羽毛球落地时距离发出点( )| A. | 6m | B. | 7m | C. | 8m | D. | 9m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com