
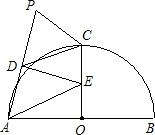
 如图,AB为半圆O的直径,OC⊥AB交⊙O于C,P为BC延长线上一动点,D为AP中点,DE⊥PA,交半径OC于E,连CD.下列结论:①PE⊥AE;②DC=DE;③∠OEA=∠APB;④PC+
如图,AB为半圆O的直径,OC⊥AB交⊙O于C,P为BC延长线上一动点,D为AP中点,DE⊥PA,交半径OC于E,连CD.下列结论:①PE⊥AE;②DC=DE;③∠OEA=∠APB;④PC+ CE为定值.其中正确结论的个数为
CE为定值.其中正确结论的个数为 ∠AEB,然后用圆周角定理得到∠APB=∠AEO.④利用③的结论,结合图形,在直角三角形中用余弦进行计算得到PC+
∠AEB,然后用圆周角定理得到∠APB=∠AEO.④利用③的结论,结合图形,在直角三角形中用余弦进行计算得到PC+ CE=
CE= OC,是圆的半径的
OC,是圆的半径的 倍,是一个定值.
倍,是一个定值.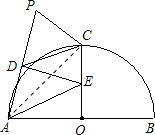 解:①如图:∵点D是AP的中点,且DE⊥AP,∴DE是AP的垂直平分线,
解:①如图:∵点D是AP的中点,且DE⊥AP,∴DE是AP的垂直平分线, ∠AEB=∠AEO,故③正确.
∠AEB=∠AEO,故③正确. AE•cos∠AE0=
AE•cos∠AE0= AE•
AE• =
= OE,
OE, CE=
CE= OE+
OE+ CE=
CE= (OE+CE)=
(OE+CE)= OC,
OC, CE为定值,是⊙O半径的
CE为定值,是⊙O半径的 倍.故④正确.
倍.故④正确.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
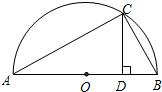 为D,AD=a,DB=b.
为D,AD=a,DB=b.| ab |
查看答案和解析>>
科目:初中数学 来源: 题型:
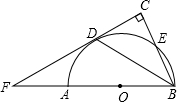 C,直线CD交BA的延长线于点F.
C,直线CD交BA的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
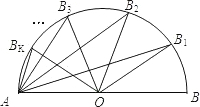 如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有
如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com