
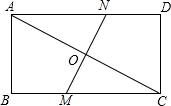
 如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD折叠,使点C与点A重合,折痕交BC于M,交AC于O,交AD于N,求:
如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD折叠,使点C与点A重合,折痕交BC于M,交AC于O,交AD于N,求:分析 (1)由勾股定理可求得AC=10,由翻折的性质可知:OA=OC=5,AC⊥MN,然后根据△OCM∽△BCA,从而可求得OM的长;
(2)然后根据三角形的面积公式和矩形的面积公式求得S△COM与S矩形ABCD的值即可求得答案.
解答 解:(1)在Rt△ABC中,由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
由翻折的性质可知:OA=OC=5,AC⊥MN.
∵∠COM=∠B=90°,∠OCM=∠BCA,
∴△OCM∽△BCA.
∴$\frac{OM}{AB}=\frac{OC}{BC}$,即$\frac{OM}{6}=\frac{5}{8}$.
解得:OM=$\frac{15}{4}$.
(2)△OCM的面积=$\frac{1}{2}OC•OM=\frac{1}{2}×5×\frac{15}{4}$=$\frac{75}{8}$.
矩形ABCD的面积=6×8=48.
∴S△COM:S矩形ABCD=$\frac{75}{8}:48$=25:128.
点评 本题主要考查的是翻折的性质、相似三角形的性质和判定、勾股定理的应用,掌握相关定理是解题的关键.


科目:初中数学 来源: 题型:填空题
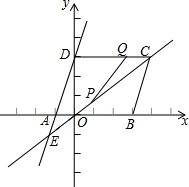 已知直线y=3x+3与x轴交于点A,与y轴交于点D,与直线y=$\frac{3}{4}$x交于点E.过点D作DC∥x轴,交直线y=$\frac{3}{4}$x于点C,过点C作CB∥AD交x轴于点B.点P从点O出发,沿线段OC向终点C运动,点Q从点C出发,沿线段CD向终点D运动.若P、Q同时出发,速度均为1单位长度/s,时间为t s.当P、Q两点有一点到达终点时,它们均停止运动.将线段PQ绕点P沿顺时针方向旋转90°.当点Q落在四边形ABCD一边所在的直线上时,t的值为2.
已知直线y=3x+3与x轴交于点A,与y轴交于点D,与直线y=$\frac{3}{4}$x交于点E.过点D作DC∥x轴,交直线y=$\frac{3}{4}$x于点C,过点C作CB∥AD交x轴于点B.点P从点O出发,沿线段OC向终点C运动,点Q从点C出发,沿线段CD向终点D运动.若P、Q同时出发,速度均为1单位长度/s,时间为t s.当P、Q两点有一点到达终点时,它们均停止运动.将线段PQ绕点P沿顺时针方向旋转90°.当点Q落在四边形ABCD一边所在的直线上时,t的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数
如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数 ,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.
,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
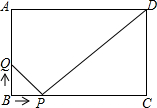 如图,长方形ABCD中,AB=4cm,BC=6cm,点P,点Q同时从点B出发,点P在线段BC上运动,点Q在线段BA上运动,它们的速度均为1cm/s,当其中一点到达端点时它们同时停止运动,设运动时间为t(s).
如图,长方形ABCD中,AB=4cm,BC=6cm,点P,点Q同时从点B出发,点P在线段BC上运动,点Q在线段BA上运动,它们的速度均为1cm/s,当其中一点到达端点时它们同时停止运动,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
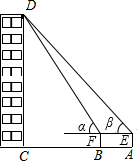 某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度.
某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com