
已知有不重合的两点A和B,以点A和点B为其中两个顶点作位置不同的等腰直角三角形,一共可以作出( )
A、2个 B、4个 C、6个 D、8个
C
【解析】
试题分析:连接AB,分别以A、B为直角顶点在AB的两边确定另一顶点位置,再以AB为斜边,再AB的两边确定另一顶点的位置,作出图形即可得解.
此题应分三种情况:
①以AB为腰,点A为直角顶点;
可作△ABC1、△ABC2,两个等腰直角三角形;
②以AB为腰,点B为直角顶点;
可作△BAC3、△BAC4,两个等腰直角三角形;
③以AB为底,点C为直角顶点;
可作△ABC5、△ABC6,两个等腰直角三角形;

综上可知,可作6个等腰直角三角形,故选C.
考点:本题考查了等腰直角三角形
点评:等腰直角三角形两腰相等,顶角为直角,据此可以构造出等腰直角三角形.难点在于分AB是直角边与斜边两种情况并且在AB的两边确定第三个顶点的位置,作出图形更形象直观.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| m |
| 2 |
| m |
| 2 |
| MA |
| AD |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012年山西省中考数学模拟试卷(四)(解析版) 题型:解答题
 经过点A,求抛物线C的函数解析式;
经过点A,求抛物线C的函数解析式;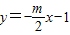 绕着点A旋转得到直线l2:y=kx+b,设直线l2与y轴交于点D,与抛物线C交于点M(M不与点A重合),当
绕着点A旋转得到直线l2:y=kx+b,设直线l2与y轴交于点D,与抛物线C交于点M(M不与点A重合),当 时,求k的取值范围.
时,求k的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com