
 .5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
.5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米? ,代入S乙=2t,
,代入S乙=2t, ,
, ,
, )
) ,解得
,解得


科目:初中数学 来源: 题型:
 .5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
.5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:
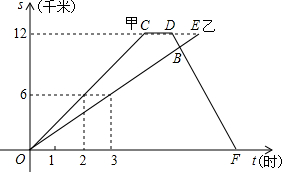
 11、甲、乙两名同学进行登山比赛,图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶过程中,各处行进的路程随时间变化的图象,根据图象中的有关数据下列问题:①甲到达山顶需要4小时;②乙到达山顶需要6小时;③甲到达山顶时,乙距山顶还有4千米;④若甲同学到达山顶后休息1小时,沿原路下山,在点B处与乙相遇,此时点B与山顶距离为1.5千米,则甲从山顶回到山脚需要2小时.其中正确的说法有( )
11、甲、乙两名同学进行登山比赛,图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶过程中,各处行进的路程随时间变化的图象,根据图象中的有关数据下列问题:①甲到达山顶需要4小时;②乙到达山顶需要6小时;③甲到达山顶时,乙距山顶还有4千米;④若甲同学到达山顶后休息1小时,沿原路下山,在点B处与乙相遇,此时点B与山顶距离为1.5千米,则甲从山顶回到山脚需要2小时.其中正确的说法有( )查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《一次函数》(04)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2005年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com