
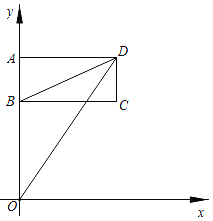
”¾ĢāÄæ”æČēĶ¼£¬³¤·½ŠĪABCDŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖµćA£Ø0£¬a£©£¬B£Ø0£¬6£©£¬C£Øb£¬6£©£¬ĒŅĀś×ća=![]() +8£®
+8£®
£Ø1£©ĒėÖ±½ÓŠ“³öA”¢C”¢DČżøöµćµÄ×ų±ź£¬A”” ””£¬C”” ””£¬D”” ””£»
£Ø2£©Į¬½ÓĻ߶ĪBD”¢OD£¬ŹŌĒóČż½ĒŠĪBODµÄĆ껿£»
£Ø3£©Čō³¤·½ŠĪABCDŅŌĆæĆė1øöµ„Ī»³¤¶ČŌČĖŁĻņĻĀŌĖ¶Æ£¬ÉčŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬ĪŹŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢ£¬Čż½ĒŠĪBODµÄĆ껿Óė³¤·½ŠĪABCDµÄĆ껿ĻąµČ£æČō“ęŌŚ£¬ĒėĒó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©A£Ø0£¬8£©£¬C£Ø4£¬6£©£¬D£Ø4£¬8£©£¬£Ø2£©12£»£Ø3£©“ęŌŚ£¬2»ņ10Ćė
”¾½āĪö”æ
£Ø1£©ĄūÓƶž“ĪøłŹ½µÄŠŌÖŹĒó³öa”¢bµÄÖµ¼“æɽā¾öĪŹĢā£»
£Ø2£©øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½¼ĘĖć¼“æÉ£»
£Ø3£©·ÖĮ½ÖÖĒéŠĪ·Ö±š¼ĘĖć¼“æÉ£»
½ā£ŗ£Ø1£©”ß a=![]() +8,
+8,
ÓÖ”ß![]()
![]() £¬
£¬
”ąb=4£¬a=8£¬
”ąA£Ø0£¬8£©£¬C£Ø4£¬6£©£¬D£Ø4£¬8£©£¬
¹Ź“š°øĪŖ£Ø0£¬8£©£¬£Ø4£¬6£©£¬£Ø4£¬8£©£»
(2)ÓÉĢāŅā£ŗ![]() .
.
£Ø3£©“ęŌŚ£®
ĄķÓÉ£ŗµ±³¤·½ŠĪABCDŌŚxÖįµÄÉĻ·½Ź±.BO=6-t,Ōņ![]() ”Į4”Į£Ø6-t£©=2”Į4,
”Į4”Į£Ø6-t£©=2”Į4,
½āµĆt=2,
µ±³¤·½ŠĪABCDŌŚxÖįµÄĻĀ·½Ź±.BO=t-6,
Ōņ![]() ”Į4£Øt-6£©=2”Į4,
”Į4£Øt-6£©=2”Į4,
½āµĆt=10,
“š£ŗŌĖ¶ÆµÄŹ±¼ä2»ņ10ĆėŹ±£¬Čż½ĒŠĪBODµÄĆ껿Óė³¤·½ŠĪABCDµÄĆ껿ĻąµČ£®


 ³å“Ģ100·Öµ„ŌŖÓÅ»ÆĮ·æ¼¾ķĻµĮŠ“š°ø
³å“Ģ100·Öµ„ŌŖÓÅ»ÆĮ·æ¼¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬”÷ABD£¬”÷ACE¶¼ŹĒµČ±ßČż½ĒŠĪ£¬
£Ø1£©ĒóÖ¤£ŗ”÷ABE”Õ”÷ADC£»
£Ø2£©Čō”ĻACD=15”ć£¬Ēó”ĻAEBµÄ¶ČŹż£»
£Ø3£©ČēĶ¼2£¬µ±”÷ABDÓė”÷ACEµÄĪ»ÖĆ·¢Éś±ä»Æ£¬Ź¹C”¢E”¢DČżµćŌŚŅ»ĢõÖ±ĻßÉĻ£¬ĒóÖ¤£ŗAC”ĪBE£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
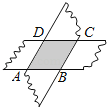
”¾ĢāÄæ”æČēĶ¼£¬¼ōĮ½ÕŶŌ±ßĘ½ŠŠµÄÖ½Ģõ£¬ĖęŅā½»²ęµž·ÅŌŚŅ»Ęš£¬×Ŗ¶ÆĘäÖŠµÄŅ»ÕÅ£¬ÖŲŗĻµÄ²æ·Ö¹¹³ÉĮĖŅ»øöĖıߊĪ£¬ÕāøöĖıߊĪŹĒ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÅ×ĪļĻßy=ax2+bx+c¾¹żA£Ø©1£¬0£©”¢B£Ø3£¬0£©”¢C£Ø0£¬3£©Čżµć£¬Ö±ĻßlŹĒÅ×ĪļĻߵĶŌ³ĘÖį£®
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ÉčµćPŹĒÖ±ĻßlÉĻµÄŅ»øö¶Æµć£¬µ±”÷PACµÄÖܳ¤×īŠ”Ź±£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ŌŚÖ±ĻßlÉĻŹĒ·ń“ęŌŚµćM£¬Ź¹”÷MACĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬Ö±½ÓŠ“³öĖłÓŠ·ūŗĻĢõ¼žµÄµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø4£©ĪŹ£ŗČōÅ×ĪļĻ߶„µćĪŖD£¬µćQĪŖÖ±ĻßACÉĻŅ»¶Æµć£¬µ±”÷DOQµÄÖܳ¤×īŠ”Ź±£¬ĒóµćQµÄ×ų±ź
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬Ņ»øöĖıߊĪÖ½Ę¬ABCD£¬”ĻB=”ĻD=90”ć£¬°ŃÖ½Ę¬°“ČēĶ¼ĖłŹ¾ÕŪµž£¬Ź¹µćBĀäŌŚAD±ßÉĻµÄB'µć£¬AEŹĒÕŪŗŪ”£

£Ø1£©ŹŌÅŠ¶ĻB'EÓėDCµÄĪ»ÖĆ¹ŲĻµ²¢ĖµĆ÷ĄķÓÉ”£
£Ø2£©Čē¹ū”ĻC=130”ć£¬Ēó”ĻAEBµÄ¶ČŹż”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ā²»µČŹ½£Ø×飩
£Ø¢ń£©½ā²»µČŹ½5x©2”Ż3£Øx+1£©£¬²¢°ŃĖüµÄ½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£®
£Ø¢ņ£©½ā²»µČŹ½×é
Ēė½įŗĻĢāŅāĢīæÕ£¬Ķź³É±¾ĢāµÄ½ā“š£®
½ā²»µČŹ½¢Ł£¬µĆ”” ””£»
½ā²»µČŹ½¢Ś£¬µĆ”” ””£»
°Ń²»µČŹ½¢ŁŗĶ¢ŚµÄ½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£ŗ
![]()
Ō²»µČŹ½×éµÄ½ā¼ÆĪŖ”” ””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬Ö±Ļß![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() .
.
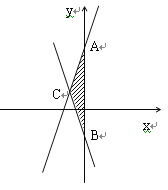
”¾1”æ£Ø1£©ĒóĮ½Ö±ĻßÓė![]() Öį½»µćA£¬BµÄ×ų±ź;
Öį½»µćA£¬BµÄ×ų±ź;
”¾2”æ£Ø2£©ĒóĮ½Ö±Ļß½»µćCµÄ×ų±ź;
”¾3”æ£Ø3£©Ēó”÷ABCµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĄķ½ā£ŗ
£Ø1£©ČēĶ¼£Ø1£©£¬µČ±ß”÷ABCÄŚÓŠŅ»µćPµ½¶„µćA£¬B£¬CµÄ¾ąĄė·Ö±šĪŖ3£¬4£¬5£¬Ōņ”ĻAPB= £®
·ÖĪö£ŗÓÉÓŚPA£¬PB²»ŌŚŅ»øöČż½ĒŠĪÖŠ£¬ĪŖĮĖ½ā¾ö±¾ĢāĪŅĆĒæÉŅŌ½«”÷ABPČʶ„µćAŠż×Ŗµ½”÷ACP”䓦£¬“ĖŹ±”÷ACP”ä”Õ £¬ ÕāŃł£¬¾ĶæÉŅŌĄūÓĆČ«µČČż½ĒŠĪÖŖŹ¶£¬½«ČżĢõĻ߶ĪµÄ³¤¶Č×Ŗ»Æµ½Ņ»øöČż½ĒŠĪÖŠ“Ó¶ųĒó³ö”ĻAPBµÄ¶ČŹż£®
£Ø2£©ĒėÄćĄūÓƵŚ£Ø1£©ĢāµÄ½ā“šĖ¼Ļė·½·Ø£¬½ā“šĻĀĆęĪŹĢā£ŗŅŃÖŖČēĶ¼£Ø2£©£¬”÷ABCÖŠ£¬”ĻCAB=90”ć£¬AB=AC£¬E”¢FĪŖBCÉĻµÄµćĒŅ”ĻEAF=45”ć£¬ĒóÖ¤£ŗBE2+CF2=EF2 £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹¤³§¼Ę»®Éś²śA£¬BĮ½ÖÖ²śĘ·¹²10¼ž£¬ĘäÉś²ś³É±¾ŗĶĄūČóČēĻĀ±ķ£ŗ
AÖÖ²śĘ· | BÖÖ²śĘ· | |
³É±¾£ØĶņŌŖ/¼ž£© | 2 | 5 |
ĄūČó£ØĶņŌŖ/¼ž£© | 1 | 3 |
£Ø1£©Čō¹¤³§¼Ę»®»ńĄū14ĶņŌŖ£¬ĪŹA£¬BĮ½ÖÖ²śĘ·Ó¦·Ö±šÉś²ś¶ąÉŁ¼ž£æ
£Ø2£©Čō¹¤³§¼Ę»®Ķ¶Čė׏½š²»¶ąÓŚ44ĶņŌŖ£¬ĒŅ»ńĄū¶ąÓŚ14ĶņŌŖ£¬ĪŹ¹¤³§ÓŠÄļøÖÖÉś²ś·½°ø£æ
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ÄÄÖÖÉś²ś·½°ø»ńĄū×ī“ó£æ²¢Ēó³ö×ī“óĄūČó£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com