
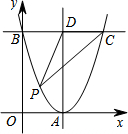
 如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B.过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(P不与B,C重合),连结PC,PD,则△PCD面积的最大值是4.
如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B.过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(P不与B,C重合),连结PC,PD,则△PCD面积的最大值是4. 分析 根据抛物线的解析式求得A、B的坐标,和对称轴方程,根据BC∥x轴,AD∥y轴对称B、C是抛物线上的对称点,所以BD=DC=2,因为顶点A到直线BC的距离最大,所以点P与A重合时,△PCD面积最大,最大值为$\frac{1}{2}$DC•AD=$\frac{1}{2}$×2×4=4.
解答 解:∵抛物线y=(x-2)2与x轴交于点A,与y轴交于点B.
∴A(2,0),B(0,4),
∵抛物线y=(x-2)2与的对称轴为x=2,BC∥x轴,AD∥y轴,
∴直线AD就是抛物线y=(x-2)2与的对称轴,
∴B、C关于直线AD对称,
∴BD=DC=2,
∵顶点A到直线BC的距离最大,
∴点P与A重合时,△PCD面积最大,最大值为$\frac{1}{2}$DC•AD=$\frac{1}{2}$×2×4=4.
故最大值为4.
点评 本题考查了二次函数图象上点的坐标特征,二次函数的性质,求得点P与A重合时,△PCD面积最大是解题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:填空题
 某区有6000名学生参加了“创建国家卫生城市”知识竞赛,为了了解本次竞赛成绩分布情况,竞赛组委会从中随机抽取部分学生的成绩(得分都是整数)作为样本,绘制成频率分布直方图如图,请根据提供的信息估计该区本次竞赛成绩在89.5分-99.5分的学生大约有900名.
某区有6000名学生参加了“创建国家卫生城市”知识竞赛,为了了解本次竞赛成绩分布情况,竞赛组委会从中随机抽取部分学生的成绩(得分都是整数)作为样本,绘制成频率分布直方图如图,请根据提供的信息估计该区本次竞赛成绩在89.5分-99.5分的学生大约有900名.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )| A. | 70° | B. | 50° | C. | 30° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,$\frac{1}{2}$) | B. | (1,2) | C. | (1,-$\frac{1}{2}$) | D. | (1,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com