
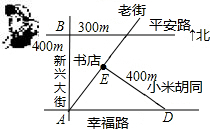
 如图,平安路与幸福路是两条平行的道路,且与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处,如果小强同学站在平安路与新兴大街的交叉路口,准备去书店,按图中的街道行走,最近的路程为500m.
如图,平安路与幸福路是两条平行的道路,且与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处,如果小强同学站在平安路与新兴大街的交叉路口,准备去书店,按图中的街道行走,最近的路程为500m. 分析 由于BC∥AD,那么有∠DAE=∠ACB,由题意可知∠ABC=∠DEA=90°,BA=ED,利用AAS可证△ABC≌△DEA,于是AE=BC=300,再利用勾股定理可求AC,即可求CE,根据图可知从B到E的走法有两种,分别计算比较即可.
解答 解:如右图所示,
∵BC∥AD,
∴∠DAE=∠ACB,
又∵BC⊥AB,DE⊥AC,
∴∠ABC=∠DEA=90°,
又∵AB=DE=400m,
∴△ABC≌△DEA,
∴EA=BC=300m,
在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=500m,
∴CE=AC-AE=200m,
从B到E有两种走法:①BA+AE=700m;②BC+CE=500m,
∴最近的路程是500m.
故答案是:500.
点评 本题考查了平行线的性质、全等三角形的判定和性质、勾股定理.解题的关键是证明△ABC≌△DEA,并能比较从B到E有两种走法.


科目:初中数学 来源: 题型:解答题
 阅读材料:
阅读材料:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com