
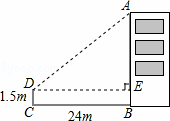
如图,为测量某建筑物的高度AB,在离该建筑物底部24米的点C处,目测建筑物顶端A处,视线与水平线夹角∠ADE为39°,且高CD为1.5米,求建筑物的高度AB.(结果精确到0.1米)(参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81)
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
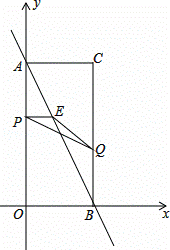
如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
对于平面直角坐标系中任意两点P1(x1,y1)、P2(x2,y2),称|x1﹣x2|+|y1﹣y2|为P1、P2两点的直角距离,记作:d(P1,P2).若P0(x0,y0)是一定点,Q(x,y)是直线y=kx+b上的一动点,称d(P0,Q)的最小值为P0到直线y=kx+b的直角距离.令P0(2,﹣3).O为坐标原点.则:
(1)d(O,P0)= ;
(2)若P(a,﹣3)到直线y=x+1的直角距离为6,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
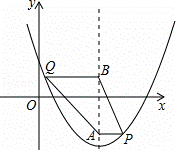
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,﹣1),且对称轴为在线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.
(1)求这条抛物线所对应的函数关系式;
(2)求点Q的坐标(用含m的式子表示);
(3)请探究PA+QB=AB是否成立,并说明理由;
(4)抛物线y=a1x2+b1x+c1(a1≠0)经过Q、B、P三点,若其对称轴把四边形PAQB分成面积为1:5的两部分,直接写出此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有( )
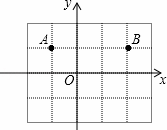
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
杨梅是漳州的特色时令水果,杨梅一上市,水果店的老板用1200元购进一批杨梅,很快售完;老板又用2500元购进第二批杨梅,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批杨梅每件进价多少元?
(2)老板以每件150元的价格销售第二批杨梅,售出80%后,为了尽快售完,决定打折促销,要使第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折?(利润=售价﹣进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com