
【题目】某校八(1)班同学为了解2018年姜堰某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 12 | 0.24 |
10<x≤15 | m | 0.32 |
15<x≤20 | 10 | n |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
(1)本次调查采用的调杳方式是 (填“普査”或“抽样调查”),样本容量是 ;
(2)补全频数分布直方图:
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“15<x≤20”的圆心角度数是 ;
(4)若该小区有5000户家庭,求该小区月均用水量超过20t的家庭大约有多少户?

【答案】(1)抽样调查,50;(2)见解析;(3)72°;(4)600(户)
【解析】
(1)由抽样调查的定义及第1组的频数与频率可得答案;
(2)根据频数=总数×频率可得m的值,据此即可补全直方图;
(3)先求得n的值,再用360°乘以n可得答案;
(4)用总户数乘以最后两组的频率之和可得答案.
解:(1)本次调查采用的调杳方式是抽样调查,样本容量为6÷0.12=50,
故答案为:抽样调查,50;
(2)m=50×0.32=16,
补全直方图如下:
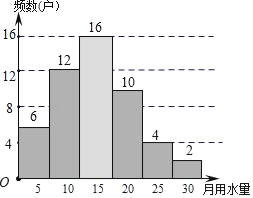
(3)∵n=10÷50=0.2,
∴月均用水量“15<x≤20”的圆心角度数是360°×0.2=72°,
故答案为:72°;
(4)该小区月均用水量超过20t的家庭大约有5000×(0.08+0.04)=600(户).


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
(1)求抛物线的函数关系式;
(2)求△MCB的面积;
(3)设点P是直线l上的一个动点,当PA+PC最小时,求最小值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.

(1)在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;
(2)连接(1)中的AA′,则线段AA′的长度是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成2块C型钢板,1块D型钢板,用1块B型钢板可制成1块C型钢板,2块D型钢板.
(1)现需要15块C型钢板,18块D型钢板,可恰好用A型钢板,B型钢板各多少块?
(2)若购买A型钢板和B型钢板共20块.要求制成C型钢板不少于25块,D型钢板不少于30块,求A、B型钢板的购买方案共有多少种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点E和点F分别在直线AB和CD上,EL和FG分别平分∠BEF和∠EFC,EL∥FG.
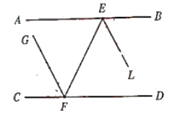
(1)求证:AB∥CD;
(2)如图,点M为FD上一点,∠BEM,∠EFD的角平分线EH,FH相交于点H,若∠H=∠FEM+15°,延长HE交FG于G点,求∠G的度数;
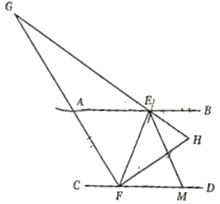
(3)如图,点N在直线AB和直线CD之间,且EN⊥FN,点P为直线AB上的点,若∠EPF,∠PFN的角平分级交于点Q,设∠BEN=α,直接写出∠PQF的大小为(用含α的式子表示).
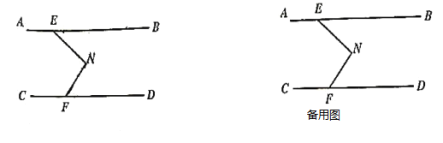
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴,y轴分别交于A,B两点,点
与x轴,y轴分别交于A,B两点,点![]() 为直线
为直线![]() 上一点,直线
上一点,直线![]() 过点C.
过点C.

![]() 求m和b的值;
求m和b的值;
![]() 直线
直线![]() 与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动
与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动![]() 设点P的运动时间为t秒.
设点P的运动时间为t秒.
①若点P在线段DA上,且![]() 的面积为10,求t的值;
的面积为10,求t的值;
②是否存在t的值,使![]() 为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
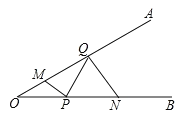
【题目】如图,∠AOB=30°,M、N分别在OA、OB上,且OM=2,ON=4,点P、Q分别在OB、OA上,则MP+PQ+QN的最小值是 _______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com