
 已知在平面直角坐标系xOy中,点A(0,2),点B(1,0),现将线段BA绕点B按顺时针方向旋转90°得到线段BD,点C为线段AB的中点,连接CD.
已知在平面直角坐标系xOy中,点A(0,2),点B(1,0),现将线段BA绕点B按顺时针方向旋转90°得到线段BD,点C为线段AB的中点,连接CD.分析 (1)求出O、C、D三点的坐标后,然后根据待定系数法即可求出该抛物线的解析式
(2)将x轴往上平移1个单位,抛物线y=ax2+x与线段CD有公共点可化为抛物线y=ax2+x-1在$\frac{1}{2}$≤x≤3上与x轴有交点,从而可求出a的范围.
解答 解:(1)过点D作DE⊥x轴于点E,如图所示.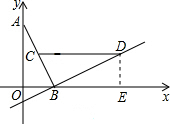
∵∠ABO+∠BAO=90°,∠ABO+∠ABD+∠DBE=180°,∠ABD=90°,
∴∠BAO=∠DBE.
在△BAO和△DBE中,$\left\{\begin{array}{l}{∠AOB=∠BED=90°}\\{∠BAO=∠DBE}\\{AB=BD}\end{array}\right.$,
∴△BAO≌△DBE(AAS),
∴BE=AO=2,DE=BO=1,OE=OB+BE=3,
∴点D(3,1).
∵点C为线段AB的中点,A(0,2),B(1,0),
∴点C($\frac{1}{2}$,1).
设过点O,C,D的抛物线的表达式为y=mx2+nx+q(m≠0),
将O(0,0)、C($\frac{1}{2}$,1)、D(3,1)代入y=mx2+nx+q,
$\left\{\begin{array}{l}{q=0}\\{\frac{1}{4}m+\frac{1}{2}n+q=1}\\{9m+3n+q=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-\frac{2}{3}}\\{n=\frac{7}{3}}\\{q=0}\end{array}\right.$,
∴过点O,C,D的抛物线的表达式为y=-$\frac{2}{3}$x2+$\frac{7}{3}$x.
故答案为:y=-$\frac{2}{3}$x2+$\frac{7}{3}$x.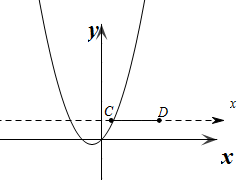
(2)∵C($\frac{1}{2}$,1)、D(3,1),
∴直线CD的表达式为y=1.
将x轴往上平移1个单位,
此时可设抛物线的解析式为:y=ax2+x+c
此时抛物线过点(0,-1)
∴c=-1,
∴将x轴往上平移1个单位后,抛物线的解析式为:y=ax2+x-1
∴抛物线y=ax2+x与线段CD有公共点可化为抛物线y=ax2+x-1在$\frac{1}{2}$≤x≤3上与x轴有交点,
∴令x=$\frac{1}{2}$代入抛物线y=ax2+x-1,
∴y=$\frac{1}{4}a+\frac{1}{2}-1$=$\frac{1}{4}$a-$\frac{1}{2}$
令x=3代入抛物线y=ax2+x-1,
∴y=9a+2
当抛物线y=ax2+x-1的对称轴不在$\frac{1}{2}$≤x≤3上时,
此时x轴有一个交点时,
∴($\frac{1}{4}$a-$\frac{1}{2}$)(9a+2)≤0,
∴-$\frac{2}{9}$≤a≤2,
当抛物线y=ax2+x-1的对称轴在$\frac{1}{2}$≤x≤3上时,
当抛物线与x轴有一个交点时,
此时△=0,
∴a=-$\frac{1}{4}$
当抛物线与x轴有两个交点时,
$\left\{\begin{array}{l}{△>0}\\{\frac{1}{2}≤-\frac{1}{2a}≤1}\\{(\frac{1}{4}a-\frac{1}{2})(9a+2)≥0}\end{array}\right.$
解得:-$\frac{1}{4}$<a<-$\frac{2}{9}$
∵综上所述,a≠0,
当抛物线y=ax2+x与线段CD有公共点时,-$\frac{1}{4}$≤a≤2且a≠0,
故答案为:(1)y=-$\frac{2}{3}$x2+$\frac{7}{3}$x;(2)-$\frac{1}{4}$≤a≤2且a≠0
点评 本题考查抛物线的综合问题,解题的关键是熟练运用 待定系数法以及抛物线的图象变换的特征,本题属于难题.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源: 题型:解答题
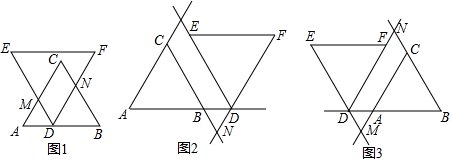
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4x-x=3 | B. | (3x2)3=9x6 | C. | (x+2)(x-2)=x2-4 | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
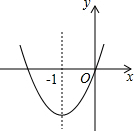 如图,已知经过原点的抛物线y-ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:①ab>0,②a+b+c>0,③当-2<x<0时,y<0,正确的结论是①②③.
如图,已知经过原点的抛物线y-ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:①ab>0,②a+b+c>0,③当-2<x<0时,y<0,正确的结论是①②③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com