
【题目】如图所示,![]() ,
,![]() 分别是正方形
分别是正方形![]() 的边
的边![]() ,
,![]() 上的点,且
上的点,且![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)若![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 为
为![]() 的中点;
的中点;
(3)连接![]() ,设
,设![]() ,
,![]() ,
,![]() ,在(2)的条件下,判断
,在(2)的条件下,判断![]() 是否成立?并说明理由.
是否成立?并说明理由.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,在等边![]() 中,点
中,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .则
.则![]() 与
与![]() 的数量关系是_____,
的数量关系是_____,![]() 的度数为______.
的度数为______.
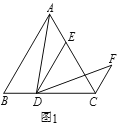
(2)拓展探究:如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,当∠ADF=∠ACF=90°时,求
,当∠ADF=∠ACF=90°时,求![]() 的值.
的值.
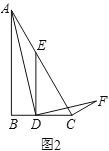
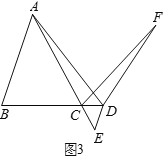
(3)解决问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,直接写出当
,直接写出当![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
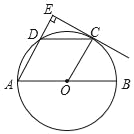
【题目】如图所示,AB是⊙O的直径,点D是弧AC的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE为⊙O的切线;
(2)若CE=![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=ax2+bx+c(a>0)的图象与x轴交于A(﹣1,0)、B(n,0)两点,一次函数y2=2x+b的图象过点A.
(1)若a=![]() ,
,
①求二次函数y1=ax2+bx+c(a>0)的函数关系式;
②设y3=y1﹣my2,是否存在正整数m,当x≥0时,y3随x的增大而增大?若存在,求出正整数m的值;若不存在,请说明理由;
(2)若![]() <a<
<a<![]() ,求证:﹣5<n<﹣4.
,求证:﹣5<n<﹣4.
查看答案和解析>>
科目:初中数学 来源: 题型:
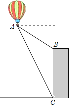
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
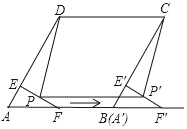
【题目】如图,在菱形ABCD中,∠A=60°,AD=4,点F是AB的中点,过点F作FE⊥AD,垂足为E,将△AEF沿点A到点B的方向平移,得到△A'E'F',设点P、P'分别是EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )
A. 7![]() B. 6
B. 6![]() C. 8
C. 8![]() D. 8
D. 8![]() ﹣4
﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知反比例函数y=![]() 的图象经过点A(1,
的图象经过点A(1,![]() ).
).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com