
【题目】通程电器商城购![]() 台空调、
台空调、![]() 台彩电需花费
台彩电需花费![]() 万元.购
万元.购![]() 台空调、
台空调、![]() 台彩电需花费
台彩电需花费![]() 万元.
万元.
(1)计算每台空调与彩电的进价分别是多少元?
(2)已知一次性购进空调、彩电共![]() 台,购进资金不超过
台,购进资金不超过![]() 万元,购进空调不少于
万元,购进空调不少于![]() 台,写出符合要求的进货方案;
台,写出符合要求的进货方案;
(3)在(2)的情况下,原每台空调的售价为![]() 元.每台彩电的售价为
元.每台彩电的售价为![]() 元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利
元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利![]() 元
元![]() .设商城计划购进空调
.设商城计划购进空调![]() 台,空调和彩电全部销售完商城获得的利润为
台,空调和彩电全部销售完商城获得的利润为![]() 元.试写出
元.试写出![]() 与
与![]() 的函数关系式,选择哪种进货方案,商城获利最大?
的函数关系式,选择哪种进货方案,商城获利最大?
【答案】(1)空调![]() 元,彩电
元,彩电![]() 元.(2)
元.(2)![]() ,
,![]() ,
,![]() ,
,![]() ,三种方案.(3)
,三种方案.(3)![]() ,当
,当![]() 时,
时,![]() 最大;当
最大;当![]() 时,
时,![]() 最大.
最大.
【解析】
(1)根据商城购3台空调、2台彩电需花费2.32万元.购2台空调、4台彩电需,花费2.48万元,可以列出相应的二元一次方程组,从而可以解答本题;
(2)根据题意可以列出相应的不等式组,从而可以求得相应的进货方案;
(3)根据题意,可以写出y与x的函数关系式,并求得选择哪种进货方案,商城获利最大.
(1)设每台空调与彩电的进价分别是x元、y元,![]()
得![]()
答:每台空调与彩电的进价分别是0.54万元、0.35万元;
故答案为:空调进价5400元,彩电进价3500元
(2)设购进空调m台,则购进彩电(30m)台,
![]()
解得,10m![]()
∵m为整数,
∴m=10,11,12,
∴共有三种进货方案,
方案一:购进空调10台,购进彩电20台,
方案二:购进空调11台,购进彩电19台,
方案三:购进空调12台,购进彩电18台;
(3)由题意可得,
y=(61005400a)x+(39003500)(30x)=(300a)x+12000,
∵![]() ,x=10,11,12,
,x=10,11,12,
∴当![]() 时,x=12时,y取得最大值,此时y=12a+15600,
时,x=12时,y取得最大值,此时y=12a+15600,
当a=300时,三种方案获利一样多,
当![]() 时,x=10时,y取得最大值,此时y=10x+15000,
时,x=10时,y取得最大值,此时y=10x+15000,
答:y与x的函数关系式是y=(300a)x+12000,当![]() 时,选择方案三:购进空调12台,购进彩电18台,商场获利最大;当a=300时,三种方案商场获利一样;当
时,选择方案三:购进空调12台,购进彩电18台,商场获利最大;当a=300时,三种方案商场获利一样;当![]() 时,选择方案一:购进空调10台,购进彩电20台,商场获利最大.
时,选择方案一:购进空调10台,购进彩电20台,商场获利最大.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】为调查七年级学生了解校园防欺凌知识的情况,小刚在主题班会后就本班学生对校园防欺凌知识的了解程度进行了一次调查统计:A:熟悉,B:较了解,C:知道.如下是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
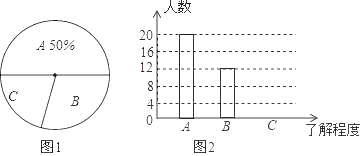
(1)求该班共有多少名学生;
(2)在条形图中将表示“知道”的部分补充完整
(3)在扇形统计图中,求“较了解”部分所对应的圆心角的度数;
(4)如果七年级共有460名同学,请你估算全年级对校园防欺凌知识“熟悉”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知直线
中,已知直线 ![]() (
( ![]() )分别交反比例函数
)分别交反比例函数 ![]() 和
和 ![]() 在第一象限的图象于点
在第一象限的图象于点 ![]() ,
, ![]() ,过点
,过点 ![]() 作
作 ![]() 轴于点
轴于点 ![]() ,交
,交 ![]() 的图象于点
的图象于点 ![]() ,连结
,连结 ![]() .若
.若 ![]() 是等腰三角形,则
是等腰三角形,则 ![]() 的值是 .
的值是 . 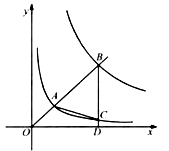
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=﹣1(a<b)的两根,则实数x1 , x2 , a,b的大小关系是( )
A.a<x1<x2<b
B.x1<a<x2<b
C.x1<a<b<x2
D.x1<x2<a<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建一条210米长的公路,甲队每天修建15米,乙队每天修建25米,一共用10天完成.
根据题意,小红和小芳同学分别列出了下面尚不完整的方程组:
小红:![]() 小芳:
小芳:
(1)请你分别写出小红和小芳所列方程组中未知数x,y表示的意义:
小红:x表示______,y表示______;
小芳:x表示______,y表示______;
(2)在题中“( )”内把小红和小芳所列方程组补充完整;
(3)甲工程队一共修建了______天,乙工程队一共修建了______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售某种玩具,进货价为20元.根据市场调查:在一段时间内,销售单价是30元时,销售量是400件,而销售单价每上涨1元,就会少售出10件玩具,超市要完成不少于300件的销售任务,又要获得最大利润,则销售单价应定为元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”. 
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A.2017
B.2016
C.191
D.190
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com