
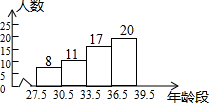
 菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )| A. | 平均年龄是37.5岁 | B. | 中位数年龄位于33.5-36.5岁 | ||
| C. | 众数年龄位于36.5-39.5岁 | D. | 以上选项都不正确 |
分析 找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
解答 解:A、平均年龄=$\frac{29×8+32×11+35×17+38×20}{56}$=$\frac{1939}{56}$=34.625岁,故本选项错误;
B、∵56名获奖者按照年龄从小到大第28、29两个人的年龄都在33.5-36.5岁这一组,
∴中位数年龄位于33.5-36.5岁,故本选项正确;
C、36.5-39.5岁这一组的人数最多,并不一定同一年龄的人数最多的也在这一组,
所以,众数年龄位于36.5-39.5岁不一定正确,故本选项错误;
D、∵B选项结论正确,
∴以上选项都不正确,错误,故本选项错误.
故选B.
点评 本题属于基础题,考查了确定一组数据的中位数和众数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
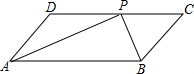 如图,在?ABCD中,∠ABC与∠BAD的平分线交于点P,且点P在CD边上.
如图,在?ABCD中,∠ABC与∠BAD的平分线交于点P,且点P在CD边上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com