
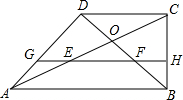
 在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F.
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F.分析 (1)先根据中位线的性质得:EF∥AB,AB=2EF,则CD∥EF,由平行线的性质得:∠ODC=∠OFE,∠OEF=∠OCD,利用ASA证明△FOE≌△DOC;
(2)分别表示出EH和CH的长,在Rt△EHC中,根据正切的定义求出结论;
(3)由(2)得结论:$GE=\frac{1}{3}CD,EF=CD,FH=\frac{1}{3}CD$,分别表示AB的长,代入$\frac{AB-CD}{GH}$求值.
解答 证明:(1)∵线段OA,OB的中点分别为E,F,
∴EF是△OAB的中位线,
∴EF∥AB,AB=2EF,
∵AB=2CD,
∴CD=EF,
∵AB∥CD,
∴CD∥EF,
∴∠ODC=∠OFE,∠OEF=∠OCD,
在△OEF和△OCD中,
∵$\left\{\begin{array}{l}{∠ODC=∠OFE}\\{DC=EF}\\{∠OCD=∠OEF}\end{array}\right.$,
∴△FOE≌△DOC(ASA);
(2)由(1)得:△FOE≌△DOC,
∴OD=OF,
∵OF=BF,
∴OF=BF=OD,
∵FH∥CD,
∴△BFH∽△BDC,
∴$\frac{FH}{CD}=\frac{BF}{BD}$=$\frac{BH}{BC}$=$\frac{1}{3}$,
∴FH=$\frac{1}{3}$CD,
∵EH=$EF+FH=CD+\frac{1}{3}CD=\frac{4}{3}CD$,
$CH=\frac{2}{3}BC=\frac{2}{3}CD$,
在Rt△EHC中,$tan∠OEF=\frac{CH}{EH}=\frac{{\frac{2}{3}CD}}{{\frac{4}{3}CD}}=\frac{1}{2}$;
(3)由(2)得:$GE=\frac{1}{3}CD,EF=CD,FH=\frac{1}{3}CD$,
∴$GH=\frac{5}{3}CD$,
又∵AB=2EF=2CD,
∴$\frac{AB-CD}{GH}=\frac{2CD-CD}{{\frac{5}{3}CD}}=\frac{3}{5}$.
点评 本题是四边形的综合题,考查了三角形的中位线定理,直角梯形的性质、三角形相似和全等的性质和判定以及三角函数的知识,在计算一个角的三角函数或求线段的和差倍商时,可以确定一个中间量,即一条线段,根据相似或全等有关边的性质将所有线段表示成某条线段的倍数关系,再约分即可.


科目:初中数学 来源: 题型:选择题
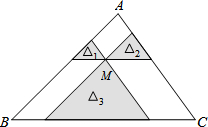 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )| A. | 62 | B. | 186 | C. | 132 | D. | 144 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:
我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com